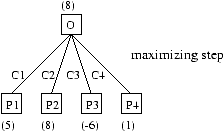
Figure 17.1: Maximizing search at a given location.



In figure 17.1, player A starts at position O, finds four legal moves, constructs these new configurations, and evaluates them. Based on these scores, the best position is P2, with a score of 8. This value is propagated to position O, indicating that this position provides a move to a new position, giving a score of 8 when the player moves to C2. The search of depth 1 is, as a general rule, insufficient, as it does not consider the possible response of an adversary. Such a shallow search results in programs that search greedily for immediate material gains (such as the prize of a queen, in chess) without perceiving that the pieces are protected or that the position is otherwise a losing one (such as a gambit of trading one's queen for a mate). A deeper exploration to depth 2 permits perceiving at least the simplest such countermoves.
Figure 17.1: Maximizing search at a given location.
Move P2, which provided an immediate position score of 8, leads to a position with a score of -3. In effect, if B plays D5, then the score of Q5 will be -3. Based on this deeper examination, the move C1 limits the losses with a score of -1, and is thus the preferred move.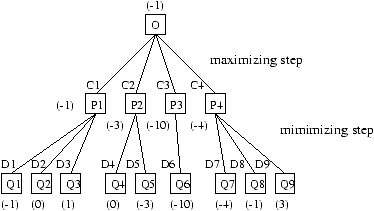
Figure 17.2: Maximizing and minimizing in depth-2 search.
As soon as the tree gets broader or deeper the number of cuts increases, thus indicating large subtrees.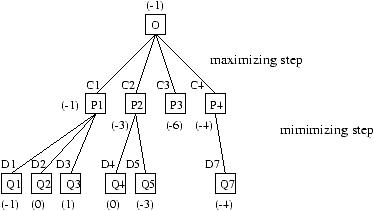
Figure 17.3: Limit a to one level max-min.
# moduletypeREPRESENTATION=sigtypegametypemovevalgame_start:unit->gamevallegal_moves:bool->game->movelistvalplay:bool->move->game->gameend;;module type REPRESENTATION =sigtype gameand moveval game_start : unit -> gameval legal_moves : bool -> game -> move listval play : bool -> move -> game -> gameend
# moduletypeEVAL=sigtypegamevalevaluate:bool->game->intvalmoreI:intvallessI:intvalis_leaf:bool->game->boolvalis_stable:bool->game->booltypestate=G|P|N|Cvalstate_of:bool->game->stateend;;module type EVAL =sigtype gameval evaluate : bool -> game -> intval moreI : intval lessI : intval is_leaf : bool -> game -> boolval is_stable : bool -> game -> booltype state = | G | P | N | Cval state_of : bool -> game -> stateend
# moduletypeALPHABETA=sigtypegametypemovevalalphabeta:int->bool->game->moveend;;module type ALPHABETA =sig type game and move val alphabeta : int -> bool -> game -> move end
# moduletypeFALPHABETA=functor(Rep:REPRESENTATION)->functor(Eval:EVALwithtypegame=Rep.game)->ALPHABETAwithtypegame=Rep.gameandtypemove=Rep.move;;module type FALPHABETA =functor(Rep : REPRESENTATION) ->functor(Eval : sigtype game = Rep.gameval evaluate : bool -> game -> intval moreI : intval lessI : intval is_leaf : bool -> game -> boolval is_stable : bool -> game -> booltype state = | G | P | N | Cval state_of : bool -> game -> stateend) ->sigtype game = Rep.gameand move = Rep.moveval alphabeta : int -> bool -> game -> moveend
# moduleFAlphabetaO(Rep:REPRESENTATION)(Eval:EVALwithtypegame=Rep.game)=structtypegame=Rep.gametypemove=Rep.moveexceptionAlphaMovementofintexceptionBetaMovementofintletmaxmin_iternodeminmax_curbetaalphacp=letalpha_resu=maxalpha(minmax_cur(Rep.playtruecpnode)betaalpha)inifalpha_resu>=betathenraise(BetaMovementalpha_resu)elsealpha_resuletminmax_iternodemaxmin_curalphabetacp=letbeta_resu=minbeta(maxmin_cur(Rep.playfalsecpnode)alphabeta)inifbeta_resu<=alphathenraise(AlphaMovementbeta_resu)elsebeta_resuletrecmaxmindepthnodealphabeta=if(depth<1&Eval.is_stabletruenode)orEval.is_leaftruenodethenEval.evaluatetruenodeelsetryletprev=maxmin_iternode(minmax(depth-1))betainList.fold_leftprevalpha(Rep.legal_movestruenode)withBetaMovementa->aandminmaxdepthnodebetaalpha=if(depth<1&Eval.is_stablefalsenode)orEval.is_leaffalsenodethenEval.evaluatefalsenodeelsetryletprev=minmax_iternode(maxmin(depth-1))alphainList.fold_leftprevbeta(Rep.legal_movesfalsenode)withAlphaMovementb->bletrecsearchal1l2=match(l1,l2)with(h1::q1,h2::q2)->ifa=h1thenh2elsesearchaq1q2|([],[])->failwith("AB: "^(string_of_inta)^" not found")|(_,_)->failwith"AB: length differs"(* val alphabeta : int -> bool -> Rep.game -> Rep.move *)letalphabetadepthplayerlevel=letalpha=refEval.lessIandbeta=refEval.moreIinletl=ref[]inletcpl=Rep.legal_movesplayerlevelinleteval=tryfori=0to(List.lengthcpl)-1doifplayerthenletb=Rep.playplayer(List.nthcpli)levelinleta=minmax(depth-1)b!beta!alphainl:=a::!l;alpha:=max!alphaa;(if!alpha>=!betathenraise(BetaMovement!alpha))elseleta=Rep.playplayer(List.nthcpli)levelinletb=maxmin(depth-1)a!alpha!betainl:=b::!l;beta:=min!betab;(if!beta<=!alphathenraise(AlphaMovement!beta))done;ifplayerthen!alphaelse!betawithBetaMovementa->a|AlphaMovementb->binl:=List.rev!l;searcheval!lcplend;;module FAlphabetaO :functor(Rep : REPRESENTATION) ->functor(Eval : sigtype game = Rep.gameval evaluate : bool -> game -> intval moreI : intval lessI : intval is_leaf : bool -> game -> boolval is_stable : bool -> game -> booltype state = | G | P | N | Cval state_of : bool -> game -> stateend) ->sigtype game = Rep.gameand move = Rep.moveexception AlphaMovement of intexception BetaMovement of intval maxmin_iter :Rep.game ->(Rep.game -> int -> int -> int) -> int -> int -> Rep.move -> intval minmax_iter :Rep.game ->(Rep.game -> int -> int -> int) -> int -> int -> Rep.move -> intval maxmin : int -> Eval.game -> int -> int -> intval minmax : int -> Eval.game -> int -> int -> intval search : int -> int list -> 'a list -> 'aval alphabeta : int -> bool -> Rep.game -> Rep.moveend
# moduleFAlphabeta=(FAlphabetaO:FALPHABETA);;module FAlphabeta : FALPHABETA
The modules with no highlighting correspond to the common parts of the application. These are the parametric modules. We see again the functor FAlphabeta. The modules with gray highlighting are the modules designed specifically for a given game. The three principal modules are the representation of the game (J_Repr), display of the game (J_Disp), and the evaluation function (J_Eval). The modules with rounded gray borders are obtained by applying the parametric modules to the simple modules specific to the game.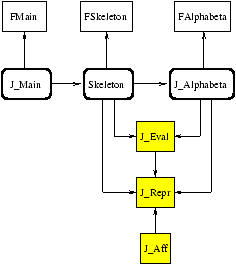
Figure 17.4: Organization of a game application.
# moduletypeSKELETON=sigvalhome:unit->unitvalinit:unit->((unit->unit)*(unit->unit))valagain:unit->boolvalexit:unit->unitvalwon:unit->unitvallost:unit->unitvalnil:unit->unitexceptionWonexceptionLostexceptionNilend;;module type SKELETON =sigval home : unit -> unitval init : unit -> (unit -> unit) * (unit -> unit)val again : unit -> boolval exit : unit -> unitval won : unit -> unitval lost : unit -> unitval nil : unit -> unitexception Wonexception Lostexception Nilend
# moduleFMain(P:SKELETON)=structletplay_gamemovements=whiletruedo(fstmovements)();(sndmovements)()doneletmain()=letfinished=reffalseinP.home();whilenot!finisheddo(tryplay_game(P.init())withP.Won->P.won()|P.Lost->P.lost()|P.Nil->P.nil());finished:=not(P.again())done;P.exit()end;;module FMain :functor(P : SKELETON) ->sigval play_game : (unit -> 'a) * (unit -> 'b) -> unitval main : unit -> unitend
# moduletypeDISPLAY=sigtypegametypemovevalhome:unit->unitvalexit:unit->unitvalwon:unit->unitvallost:unit->unitvalnil:unit->unitvalinit:unit->unitvalposition:bool->move->game->game->unitvalchoice:bool->game->movevalq_player:unit->boolvalq_begin:unit->boolvalq_continue:unit->boolend;;module type DISPLAY =sigtype gameand moveval home : unit -> unitval exit : unit -> unitval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval init : unit -> unitval position : bool -> move -> game -> game -> unitval choice : bool -> game -> moveval q_player : unit -> boolval q_begin : unit -> boolval q_continue : unit -> boolend
# moduleFSkeleton(Rep:REPRESENTATION)(Disp:DISPLAYwithtypegame=Rep.gameandtypemove=Rep.move)(Eval:EVALwithtypegame=Rep.game)(Alpha:ALPHABETAwithtypegame=Rep.gameandtypemove=Rep.move)=structletdepth=ref4exceptionWonexceptionLostexceptionNilletwon=Disp.wonletlost=Disp.lostletnil=Disp.nilletagain=Disp.q_continueletplay_game=ref(Rep.game_start())letexit=Disp.exitlethome=Disp.homeletplayHplayer()=letchoice=Disp.choiceplayer!play_gameinletold_game=!play_gameinplay_game:=Rep.playplayerchoice!play_game;Disp.positionplayerchoiceold_game!play_game;matchEval.state_ofplayer!play_gamewithEval.P->raiseLost|Eval.G->raiseWon|Eval.N->raiseNil|_->()letplayMplayer()=letchoice=Alpha.alphabeta!depthplayer!play_gameinletold_game=!play_gameinplay_game:=Rep.playplayerchoice!play_game;Disp.positionplayerchoiceold_game!play_game;matchEval.state_ofplayer!play_gamewithEval.G->raiseWon|Eval.P->raiseLost|Eval.N->raiseNil|_->()letinit()=leta=Disp.q_player()inletb=Disp.q_player()inplay_game:=Rep.game_start();Disp.init();match(a,b)withtrue,true->playMtrue,playMfalse|true,false->playMtrue,playHfalse|false,true->playHtrue,playMfalse|false,false->playHtrue,playHfalseend;;module FSkeleton :functor(Rep : REPRESENTATION) ->functor(Disp : sigtype game = Rep.gameand move = Rep.moveval home : unit -> unitval exit : unit -> unitval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval init : unit -> unitval position : bool -> move -> game -> game -> unitval choice : bool -> game -> moveval q_player : unit -> boolval q_begin : unit -> boolval q_continue : unit -> boolend) ->functor(Eval : sigtype game = Rep.gameval evaluate : bool -> game -> intval moreI : intval lessI : intval is_leaf : bool -> game -> boolval is_stable : bool -> game -> booltype state = | G | P | N | Cval state_of : bool -> game -> stateend) ->functor(Alpha : sigtype game = Rep.gameand move = Rep.moveval alphabeta : int -> bool -> game -> moveend) ->sigval depth : int refexception Wonexception Lostexception Nilval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval again : unit -> boolval play_game : Disp.game refval exit : unit -> unitval home : unit -> unitval playH : bool -> unit -> unitval playM : bool -> unit -> unitval init : unit -> (unit -> unit) * (unit -> unit)end
Note the ``winning'' line of four gray pieces in a diagonal, going down and to the right.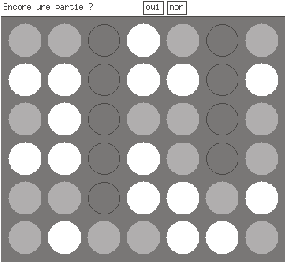
Figure 17.5: An example of Connect Four.
# moduleC4_rep=structtypecell=A|B|Emptytypegame=cellarrayarraytypemove=intletcol=7androw=6letgame_start()=Array.create_matrixrowcolEmptyletlegal_movesbm=letl=ref[]inforc=0tocol-1doifm.(row-1).(c)=Emptythenl:=(c+1)::!ldone;!lletaugmentmatc=letl=refrowinwhile!l>0&mat.(!l-1).(c-1)=Emptydodecrldone;!l+1letplayer_gencpme=letmj=Array.mapArray.copyminmj.((augmentmjcp)-1).(cp-1)<-e;mjletplaybcpm=ifbthenplayer_gencpmAelseplayer_gencpmBend;;module C4_rep :sigtype cell = | A | B | Emptyand game = cell array arrayand move = intval col : intval row : intval game_start : unit -> cell array arrayval legal_moves : 'a -> cell array array -> int listval augment : cell array array -> int -> intval player_gen : int -> cell array array -> cell -> cell array arrayval play : bool -> int -> cell array array -> cell array arrayend
# moduleC4_rep_T=(C4_rep:REPRESENTATION);;module C4_rep_T : REPRESENTATION
# moduleC4_text=structopenC4_reptypegame=C4_rep.gametypemove=C4_rep.moveletprint_gamemat=forl=row-1downto0doforc=0tocol-1domatchmat.(l).(c)withA->print_string"X "|B->print_string"O "|Empty->print_string". "done;print_newline()done;print_newline()lethome()=print_string"C4 ...\n"letexit()=print_string"Bye for now ... \n"letquestions=print_strings;print_string" y/n ? ";read_line()="y"letq_begin()=question"Would you like to begin?"letq_continue()=question"Play again?"letq_player()=question"Is there to be a machine player ?"letwon()=print_string"The first player won";print_newline()letlost()=print_string"The first player lost";print_newline()letnil()=print_string"Stalemate";print_newline()letinit()=print_string"X: 1st player O: 2nd player";print_newline();print_newline();print_game(game_start());print_newline()letpositionbcajj=print_gamejletis_move=function'1'..'7'->true|_->falseexceptionMoveofintletrecchoiceplayergame=print_string("Choose player"^(ifplayerthen"1"else"2")^" : ");letl=legal_movesplayergameintrywhiletruedoleti=read_line()in(if(String.lengthi>0)&&(is_movei.[0])thenletc=(int_of_chari.[0])-(int_of_char'0')inifList.memclthenraise(Movec));print_string"Invalid move - try again"done;List.hdlwithMovei->i|_->List.hdlend;;module C4_text :sigtype game = C4_rep.gameand move = C4_rep.moveval print_game : C4_rep.cell array array -> unitval home : unit -> unitval exit : unit -> unitval question : string -> boolval q_begin : unit -> boolval q_continue : unit -> boolval q_player : unit -> boolval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval init : unit -> unitval position : 'a -> 'b -> 'c -> C4_rep.cell array array -> unitval is_move : char -> boolexception Move of intval choice : bool -> C4_rep.cell array array -> intend
# moduleC4_text_T=(C4_text:DISPLAY);;module C4_text_T : DISPLAY
# moduleC4_eval=structopenC4_reptypegame=C4_rep.gameletvalue=Array.of_list[0;2;10;50]exceptionFourofintexceptionNil_ValueexceptionArg_invalidletlessI=-10000letmoreI=10000leteval_fourml_depc_depdelta_ldelta_c=letn=ref0ande=refEmptyandx=refc_depandy=refl_depintryfori=1to4doif!y<0or!y>=rowor!x<0or!x>=colthenraiseArg_invalid;(matchm.(!y).(!x)withA->if!e=BthenraiseNil_Value;incrn;if!n=4thenraise(FourmoreI);e:=A|B->if!e=AthenraiseNil_Value;incrn;if!n=4thenraise(FourlessI);e:=B;|Empty->());x:=!x+delta_c;y:=!y+delta_ldone;value.(!n)*(if!e=Athen1else-1)withNil_Value|Arg_invalid->0leteval_blocmecmincmaxlminlmaxdxdy=forc=cmintocmaxdoforl=lmintolmaxdoe:=!e+eval_fourmlcdxdydonedoneletevaluatebm=tryletevaluation=ref0in(* evaluation of rows *)eval_blocmevaluation0(row-1)0(col-4)01;(* evaluation of columns *)eval_blocmevaluation0(col-1)0(row-4)10;(* diagonals coming from the first line (to the right) *)eval_blocmevaluation0(col-4)0(row-4)11;(* diagonals coming from the first line (to the left) *)eval_blocmevaluation1(row-4)0(col-4)11;(* diagonals coming from the last line (to the right) *)eval_blocmevaluation3(col-1)0(row-4)1(-1);(* diagonals coming from the last line (to the left) *)eval_blocmevaluation1(row-4)3(col-1)1(-1);!evaluationwithFourv->vletis_leafbm=letv=evaluatebminv=moreIorv=lessIorlegal_movesbm=[]letis_stablebj=truetypestate=G|P|N|Cletstate_ofplayerm=letv=evaluateplayerminifv=moreIthenifplayerthenGelsePelseifv=lessIthenifplayerthenPelseGelseiflegal_movesplayerm=[]thenNelseCend;;module C4_eval :sigtype game = C4_rep.gameval value : int arrayexception Four of intexception Nil_Valueexception Arg_invalidval lessI : intval moreI : intval eval_four :C4_rep.cell array array -> int -> int -> int -> int -> intval eval_bloc :C4_rep.cell array array ->int ref -> int -> int -> int -> int -> int -> int -> unitval evaluate : 'a -> C4_rep.cell array array -> intval is_leaf : 'a -> C4_rep.cell array array -> boolval is_stable : 'a -> 'b -> booltype state = | G | P | N | Cval state_of : bool -> C4_rep.cell array array -> stateend
# moduleC4_eval_T=(C4_eval:EVAL);;module C4_eval_T : EVAL
# moduleC4_skeleton=FSkeleton(C4_rep)(C4_text)(C4_eval)(FAlphabeta(C4_rep)(C4_eval));;module C4_skeleton :sigval depth : int refexception Wonexception Lostexception Nilval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval again : unit -> boolval play_game : C4_text.game refval exit : unit -> unitval home : unit -> unitval playH : bool -> unit -> unitval playM : bool -> unit -> unitval init : unit -> (unit -> unit) * (unit -> unit)end
# moduleC4_main=FMain(C4_skeleton);;module C4_main :sigval play_game : (unit -> 'a) * (unit -> 'b) -> unitval main : unit -> unitend
# C4_main.main () ;; C4 ... Is there to be a machine player ? y/n ? y Is there to be a machine player ? y/n ? y X: 1st player O: 2nd player . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Once the initial position is played, player 1 (controlled by the program) calculates its move which is then applied.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . X .Player 2 (always controlled by the program) calculates its response and the game proceeds, until a game-ending move is found. In this example, player 1 wins the game based on the following final position:
. O O O . O . . X X X . X . X O O X . O . X X X O . X . X O O X X O . X O O O X X O Player 1 wins Play again(y/n) ? n Good-bye ... - : unit = ()
# moduleC4_graph=structopenC4_reptypegame=C4_rep.gametypemove=C4_rep.moveletr=20(* color of piece *)letec=10(* distance between pieces *)letdec=30(* center of first piece *)letcote=2*r+ec(* height of a piece looked at like a checker *)lethtexte=25(* where to place text *)letwidth=col*cote+ec(* width of the window *)letheight=row*cote+ec+htexte(* height of the window *)letheight_of_game=row*cote+ec(* height of game space *)lethec=height_of_game+7(* line for messages *)letlec=3(* columns for messages *)letmargin=4(* margin for buttons *)letxb1=width/2(* position x of button1 *)letxb2=xb1+30(* position x of button2 *)letyb=hec-margin(* position y of the buttons *)letwb=25(* width of the buttons *)lethb=16(* height of the buttons *)(* val t2e : int -> int *)(* Convert a matrix coordinate into a graphical coordinate *)lett2ei=dec+(i-1)*cote(* The Colors *)letcN=Graphics.black(* trace *)letcA=Graphics.red(* Human player *)letcB=Graphics.yellow(* Machine player *)letcF=Graphics.blue(* Game Background color *)(* val draw_table : unit -> unit : Trace an empty table *)letdraw_table()=Graphics.clear_graph();Graphics.set_colorcF;Graphics.fill_rect00widthheight_of_game;Graphics.set_colorcN;Graphics.moveto0height_of_game;Graphics.linetowidthheight_of_game;forl=1torowdoforc=1tocoldoGraphics.draw_circle(t2ec)(t2el)rdonedone(* val draw_piece : int -> int -> Graphics.color -> unit *)(* 'draw_piece l c co' draws a piece of color co at coordinates l c *)letdraw_piecelccol=Graphics.set_colorcol;Graphics.fill_circle(t2ec)(t2el)(r+1)(* val augment : Rep.item array array -> int -> Rep.move *)(* 'augment m c' redoes the line or drops the piece for c in m *)letaugmentmatc=letl=refrowinwhile!l>0&mat.(!l-1).(c-1)=Emptydodecrldone;!l(* val conv : Graphics.status -> int *)(* convert the region where player has clicked in controlling the game *)letconvst=(st.Graphics.mouse_x-5)/50+1(* val wait_click : unit -> Graphics.status *)(* wait for a mouse click *)letwait_click()=Graphics.wait_next_event[Graphics.Button_down](* val choiceH : Rep.game -> Rep.move *)(* give opportunity to the human player to choose a move *)(* the function offers possible moves *)letrecchoiceplayergame=letc=ref0inwhilenot(List.mem!c(legal_movesplayergame))doc:=conv(wait_click())done;!c(* val home : unit -> unit : home screen *)lethome()=Graphics.open_graph(" "^(string_of_intwidth)^"x"^(string_of_intheight)^"+50+50");Graphics.moveto(height/2)(width/2);Graphics.set_colorcF;Graphics.draw_string"C4";Graphics.set_colorcN;Graphics.moveto22;Graphics.draw_string"by Romuald COEFFIER & Mathieu DESPIERRE";ignore(wait_click());Graphics.clear_graph()(* val end : unit -> unit , the end of the game *)letexit()=Graphics.close_graph()(* val draw_button : int -> int -> int -> int -> string -> unit *)(* 'draw_button x y w h s' draws a rectangular button at coordinates *)(* x,y with width w and height h and appearance s *)letdraw_buttonxywhs=Graphics.set_colorcN;Graphics.movetoxy;Graphics.linetox(y+h);Graphics.lineto(x+w)(y+h);Graphics.lineto(x+w)y;Graphics.linetoxy;Graphics.moveto(x+margin)(hec);Graphics.draw_strings(* val draw_message : string -> unit * position message s *)letdraw_messages=Graphics.set_colorcN;Graphics.movetolechec;Graphics.draw_strings(* val erase_message : unit -> unit erase the starting position *)leterase_message()=Graphics.set_colorGraphics.white;Graphics.fill_rect0(height_of_game+1)widthhtexte(* val question : string -> bool *)(* 'question s' poses the question s, the response being obtained by *)(* selecting one of two buttons, 'yes' (=true) and 'no' (=false) *)letquestions=letrecattente()=lete=wait_click()inif(e.Graphics.mouse_y<(yb+hb))&(e.Graphics.mouse_y>yb)thenif(e.Graphics.mouse_x>xb1)&(e.Graphics.mouse_x<(xb1+wb))thentrueelseif(e.Graphics.mouse_x>xb2)&(e.Graphics.mouse_x<(xb2+wb))thenfalseelseattente()elseattente()indraw_messages;draw_buttonxb1ybwbhb"yes";draw_buttonxb2ybwbhb"no";attente()(* val q_begin : unit -> bool *)(* Ask, using function 'question', if the player wishes to start *)(* (yes=true) *)letq_begin()=letb=question"Would you like to begin ?"inerase_message();b(* val q_continue : unit -> bool *)(* Ask, using function 'question', if the player wishes to play again *)(* (yes=true) *)letq_continue()=letb=question"Play again ?"inerase_message();bletq_player()=letb=question"Is there to be a machine player?"inerase_message();b(* val won : unit -> unit *)(* val lost : unit -> unit *)(* val nil : unit -> unit *)(* Three functions for these three cases *)letwon()=draw_message"I won :-)";ignore(wait_click());erase_message()letlost()=draw_message"You won :-(";ignore(wait_click());erase_message()letnil()=draw_message"Stalemate";ignore(wait_click());erase_message()(* val init : unit -> unit *)(* This is called at every start of the game for the position *)letinit=draw_tableletpositionbcajnj=ifbthendraw_piece(augmentnjc)ccAelsedraw_piece(augmentnjc)ccB(* val drawH : int -> Rep.item array array -> unit *)(* Position when the human player chooses move cp in situation j *)letdrawHcpj=draw_piece(augmentjcp)cpcA(* val drawM : int -> cell array array -> unit*)(* Position when the machine player chooses move cp in situation j *)letdrawMcpj=draw_piece(augmentjcp)cpcBend;;module C4_graph :sigtype game = C4_rep.gameand move = C4_rep.moveval r : intval ec : intval dec : intval cote : intval htexte : intval width : intval height : intval height_of_game : intval hec : intval lec : intval margin : intval xb1 : intval xb2 : intval yb : intval wb : intval hb : intval t2e : int -> intval cN : Graphics.colorval cA : Graphics.colorval cB : Graphics.colorval cF : Graphics.colorval draw_table : unit -> unitval draw_piece : int -> int -> Graphics.color -> unitval augment : C4_rep.cell array array -> int -> intval conv : Graphics.status -> intval wait_click : unit -> Graphics.statusval choice : 'a -> C4_rep.cell array array -> intval home : unit -> unitval exit : unit -> unitval draw_button : int -> int -> int -> int -> string -> unitval draw_message : string -> unitval erase_message : unit -> unitval question : string -> boolval q_begin : unit -> boolval q_continue : unit -> boolval q_player : unit -> boolval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval init : unit -> unitval position : bool -> int -> 'a -> C4_rep.cell array array -> unitval drawH : int -> C4_rep.cell array array -> unitval drawM : int -> C4_rep.cell array array -> unitend
# moduleC4_skeletonG=FSkeleton(C4_rep)(C4_graph)(C4_eval)(FAlphabeta(C4_rep)(C4_eval));;
# moduleC4_mainG=FMain(C4_skeletonG);;module C4_mainG :sigval play_game : (unit -> 'a) * (unit -> 'b) -> unitval main : unit -> unitend
In turn, each player places one of his 9 pieces, numbered from 1 to 6, on one of the 18 gray internal positions. They may not place a piece on a position that is already occupied. Each time a piece is placed, one or several ley-lines may be won or lost.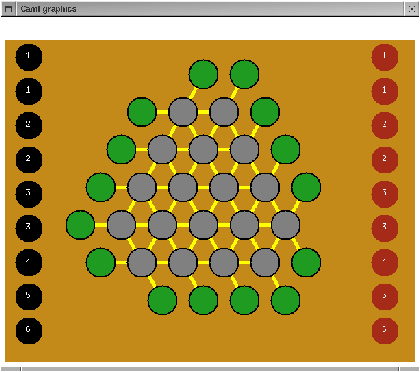
Figure 17.6: Initial position of Stonehenge.
In the case where the scores are equal across a full line, whoever placed the last piece without having beaten his adversary's score, loses the line. Figure 17.8 demonstrates such a situation.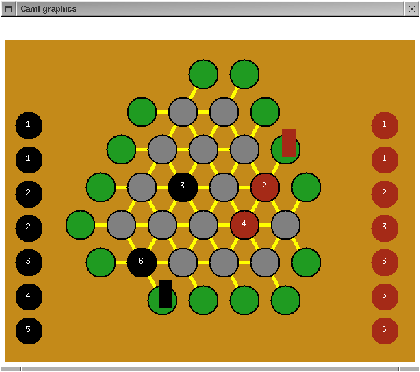
Figure 17.7: Position after 4 moves.
There can never be a tie in this game. There are 15 lines, each of which will be accounted for at some point in the game, at which point one of the players will have won at least 8 lines.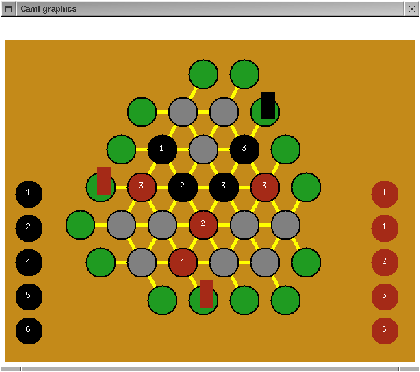
Figure 17.8: Position after 6 moves.
1---2
/ \ / \
3---4---5
/ \ / \ / \
6---7---8---9
/ \ / \ / \ / \
10--11--12--13--14
\ / \ / \ / \ /
15--16--17--18
Each location participates in 3 ley-lines. We also number each
ley-line. This description may be found in the declaration of the
list lines, which is converted to a vector
(vector_l). A location is either empty, or contains a
piece that has been placed, and the piece's possessor. We also store,
for each location, the number of the lines that pass through it.
This table is calculated by
lines_per_case and is named
num_line_per_case.# moduleStone_rep=structtypeplayer=booltypepiece=Pofintletint_of_piece=functionPx->xtypeplacement=None|Mofplayertypecase=Empty|Occupofplayer*pieceletvalue_on_case=functionEmpty->0|Occup(j,x)->int_of_piecextypegame=Jofcasearray*placementarray*piecelist*piecelisttypemove=int*pieceletlines=[[0;1];[2;3;4];[5;6;7;8;];[9;10;11;12;13];[14;15;16;17];[0;2;5;9];[1;3;6;10;14];[4;7;11;15];[8;12;16];[13;17];[9;14];[5;10;15];[2;6;11;16];[0;3;7;12;17];[1;4;8;13]]letvector_l=Array.of_listlinesletlines_per_casev=lett=Array.lengthvinletr=Array.create18[||]infori=0to17doletw=Array.create30andp=ref0inforj=0tot-1doifList.memiv.(j)then(w.(!p)<-j;incrp)done;r.(i)<-wdone;rletnum_line_per_case=lines_per_casevector_lletreclines_of_iil=List.filter(funt->List.memit)lletlines_of_casesl=leta=Array.create18linfori=0to17doa.(i)<-(lines_of_iil)done;aletldc=lines_of_caseslinesletgame_start()=letlp=[6;5;4;3;3;2;2;1;1]inJ(Array.create18Empty,Array.create15None,List.map(funx->Px)lp,List.map(funx->Px)lp)letrecunicityl=matchlwith[]->[]|h::t->ifList.memhtthenunicitytelseh::(unicityt)letlegal_movesplayer(J(ca,m,r1,r2))=letr=ifplayerthenr1elser2inifr=[]then[]elseletl=ref[]infori=0to17doifvalue_on_caseca.(i)=0thenl:=i::!ldone;letl2=List.map(funx->List.map(funy->x,y)(List.rev(unicityr)))!linList.flattenl2letcopy_boardp=Array.copypletcarn_copym=Array.copymletrecplay_piecestonel=matchlwith[]->[]|x::q->ifx=stonethenqelsex::(play_piecestoneq)letcount_caseplayercase=matchcasewithEmpty->0|Occup(j,p)->ifj=playerthen(int_of_piecep)else0letcount_lineplayerlinepos=List.fold_left(funxy->x+count_caseplayerpos.(y))0lineletreccount_maxn=function[]->0|t::q->if(n>0)then(int_of_piecet)+count_max(n-1)qelse0letrecnbr_cases_freecal=matchlwith[]->0|t::q->letc=ca.(t)inmatchcwithEmpty->1+nbr_cases_freecaq|_->nbr_cases_freecaqleta_placementima=matchma.(i)withNone->false|_->trueletwhich_placementima=matchma.(i)withNone->failwith"which_placement"|Mj->jletis_filledlca=nbr_cases_freecal=0(* function play : arbitrates the game *)letplayplayermovegame=let(c,i)=moveinletJ(p,m,r1,r2)=gameinletnr1,nr2=ifplayerthenplay_pieceir1,r2elser1,play_pieceir2inletnp=copy_boardpinletnm=carn_copyminnp.(c)<-Occup(player,i);(* on play le move *)letlines_of_the_case=num_line_per_case.(c)in(* calculation of the placements of the three lines *)fork=0to2doletl=lines_of_the_case.(k)inifnot(a_placementlnm)then(ifis_filledvector_l.(l)npthen(letc1=count_lineplayervector_l.(l)npandc2=count_line(notplayer)vector_l.(l)npinif(c1>c2)thennm.(l)<-Mplayerelse(ifc2>c1thennm.(l)<-M(notplayer)elsenm.(l)<-M(notplayer))))done;(* calculation of other placements *)fork=0to14doifnot(a_placementknm)thenifis_filledvector_l.(k)npthenfailwith"player"elseletc1=count_lineplayervector_l.(k)npandc2=count_line(notplayer)vector_l.(k)npinletcases_free=nbr_cases_freenpvector_l.(k)inletmax1=count_maxcases_free(ifplayerthennr1elsenr2)andmax2=count_maxcases_free(ifplayerthennr2elsenr1)inifc1>=c2+max2thennm.(k)<-Mplayerelseifc2>=c1+max1thennm.(k)<-M(notplayer)done;J(np,nm,nr1,nr2)end;;module Stone_rep :sigtype player = booland piece = | P of intval int_of_piece : piece -> inttype placement = | None | M of playerand case = | Empty | Occup of player * pieceval value_on_case : case -> inttype game = | J of case array * placement array * piece list * piece listand move = int * pieceval lines : int list listval vector_l : int list arrayval lines_per_case : int list array -> int array arrayval num_line_per_case : int array arrayval lines_of_i : 'a -> 'a list list -> 'a list listval lines_of_cases : int list list -> int list list arrayval ldc : int list list arrayval game_start : unit -> gameval unicity : 'a list -> 'a listval legal_moves : bool -> game -> (int * piece) listval copy_board : 'a array -> 'a arrayval carn_copy : 'a array -> 'a arrayval play_piece : 'a -> 'a list -> 'a listval count_case : player -> case -> intval count_line : player -> int list -> case array -> intval count_max : int -> piece list -> intval nbr_cases_free : case array -> int list -> intval a_placement : int -> placement array -> boolval which_placement : int -> placement array -> playerval is_filled : int list -> case array -> boolval play : player -> int * piece -> game -> gameend
# moduleStone_eval=structopenStone_reptypegame=Stone_rep.gameexceptionDoneofboolletmoreI=1000andlessI=-1000letnbr_lines_won(J(ca,m,r1,r2))=letc1,c2=ref0,ref0infori=0to14doifa_placementimthenifwhich_placementimthenincrc1elseincrc2done;!c1,!c2letrecnbr_points_remaininglig=matchligwith[]->0|t::q->(int_of_piecet)+nbr_points_remainingqletevaluateplayergame=let(J(ca,ma,r1,r2))=gameinletc1,c2=nbr_lines_wongameinletpr1,pr2=nbr_points_remainingr1,nbr_points_remainingr2inmatchplayerwithtrue->ifc1>7thenmoreIelse50*(c1-c2)+10*(pr1-pr2)|false->ifc2>7thenlessIelse50*(c1-c2)+10*(pr1-pr2)letis_leafplayergame=letv=evaluateplayergameinv=moreIorv=lessIorlegal_movesplayergame=[]letis_stableplayergame=truetypestate=G|P|N|Cletstate_ofplayerm=letv=evaluateplayerminifv=moreIthenifplayerthenGelsePelseifv=lessIthenifplayerthenPelseGelseiflegal_movesplayerm=[]thenNelseCend;;module Stone_eval :sigtype game = Stone_rep.gameexception Done of boolval moreI : intval lessI : intval nbr_lines_won : Stone_rep.game -> int * intval nbr_points_remaining : Stone_rep.piece list -> intval evaluate : bool -> Stone_rep.game -> intval is_leaf : bool -> Stone_rep.game -> boolval is_stable : 'a -> 'b -> booltype state = | G | P | N | Cval state_of : bool -> Stone_rep.game -> stateend
# moduleStone_graph=structopenStone_reptypepiece=Stone_rep.piecetypeplacement=Stone_rep.placementtypecase=Stone_rep.casetypegame=Stone_rep.gametypemove=Stone_rep.move(* brightness for a piece *)letbrightness=20(* the colors *)letcBlack=Graphics.blackletcRed=Graphics.rgb1654324letcYellow=Graphics.yellowletcGreen=Graphics.rgb3115533(*Graphics.green*)letcWhite=Graphics.whiteletcGray=Graphics.rgb128128128letcBlue=Graphics.rgb19613925(*Graphics.blue*)(* width and height *)letwidth=600letheight=500(* the border at the top of the screen from which drawing begins *)lettop_offset=30(* height of foundaries *)letbounds=5(* the size of the border on the left side of the virtual table *)letvirtual_table_xoffset=145(* left shift for the black pieces *)letchoice_black_offset=40(* left shift for the red pieces *)letchoice_red_offset=560(* height of a case for the virtual table *)letvirtual_case_size=60(* corresp : int*int -> int*int *)(* establishes a correspondence between a location in the matrix *)(* and a position on the virtual table servant for drawing *)letcorrespcp=matchcpwith0->(4,1)|1->(6,1)|2->(3,2)|3->(5,2)|4->(7,2)|5->(2,3)|6->(4,3)|7->(6,3)|8->(8,3)|9->(1,4)|10->(3,4)|11->(5,4)|12->(7,4)|13->(9,4)|14->(2,5)|15->(4,5)|16->(6,5)|17->(8,5)|_->(0,0)letcorresp2((x,y)ascp)=matchcpwith(0,0)->0|(0,1)->1|(1,0)->2|(1,1)->3|(1,2)->4|(2,0)->5|(2,1)->6|(2,2)->7|(2,3)->8|(3,0)->9|(3,1)->10|(3,2)->11|(3,3)->12|(3,4)->13|(4,0)->14|(4,1)->15|(4,2)->16|(4,3)->17|(x,y)->print_string"Err ";print_intx;print_string" ";print_inty;print_newline();0letcol=5letlig=5(* draw_background : unit -> unit *)(* draw the screen background *)letdraw_background()=Graphics.clear_graph();Graphics.set_colorcBlue;Graphics.fill_rectboundsboundswidth(height-top_offset)(* draw_places : unit -> unit *)(* draw the pieces at the start of the game *)letdraw_places()=forl=0to17doletcp=corresplinifcp<>(0,0)thenbeginGraphics.set_colorcBlack;Graphics.draw_circle((fstcp)*30+virtual_table_xoffset)(height-((sndcp)*55+25)-50)(brightness+1);Graphics.set_colorcGray;Graphics.fill_circle((fstcp)*30+virtual_table_xoffset)(height-((sndcp)*55+25)-50)brightnessenddone(* draw_force_lines : unit -> unit *)(* draws ley-lines *)letdraw_force_lines()=Graphics.set_colorcYellow;letlst=[((2,1),(6,1));((1,2),(7,2));((0,3),(8,3));((-1,4),(9,4));((0,5),(8,5));((5,0),(1,4));((7,0),(2,5));((8,1),(4,5));((9,2),(6,5));((10,3),(8,5));((3,6),(1,4));((5,6),(2,3));((7,6),(3,2));((9,6),(4,1));((10,5),(6,1))]inletreclinesl=matchlwith[]->()|h::t->letdeb=fsthandcomplete=sndhinGraphics.moveto((fstdeb)*30+virtual_table_xoffset)(height-((snddeb)*55+25)-50);Graphics.lineto((fstcomplete)*30+virtual_table_xoffset)(height-((sndcomplete)*55+25)-50);linestinlineslst(* draw_final_places : unit -> unit *)(* draws final cases for each ley-line *)(* coordinates represent in the virtual arrayused for positioning *)letdraw_final_places()=letlst=[(2,1);(1,2);(0,3);(-1,4);(0,5);(3,6);(5,6);(7,6);(9,6);(10,5);(10,3);(9,2);(8,1);(7,0);(5,0)]inletrecfinall=matchlwith[]->()|h::t->Graphics.set_colorcBlack;Graphics.draw_circle((fsth)*30+virtual_table_xoffset)(height-((sndh)*55+25)-50)(brightness+1);Graphics.set_colorcGreen;Graphics.fill_circle((fsth)*30+virtual_table_xoffset)(height-((sndh)*55+25)-50)brightness;finaltinfinallst(* draw_table : unit -> unit *)(* draws the whole game *)letdraw_table()=Graphics.set_colorcYellow;draw_background();Graphics.set_line_width5;draw_force_lines();Graphics.set_line_width2;draw_places();draw_final_places();Graphics.set_line_width1(* move -> couleur -> unit *)letdraw_pieceplayer(n_case,Pcp)=(* (n_caOccup(c,v),cp) col =*)Graphics.set_color(ifplayerthencBlackelsecRed);(*col;*)letco=correspn_caseinletx=((fstco)*30+145)andy=(height-((sndco)*55+25)-50)inGraphics.fill_circlexybrightness;Graphics.set_colorcWhite;Graphics.moveto(x-3)(y-3);letdummy=5inGraphics.draw_string(string_of_intcp)(*;*)(* print_string "---";print_int n_case; print_string " "; print_int cp ;print_newline() *)(* conv : Graphics.status -> int *)(* convert a mouse click into a position on a virtual table permitting *)(* its drawing *)letconvst=letxx=st.Graphics.mouse_xandyy=st.Graphics.mouse_yinlety=(yy+10)/virtual_case_size-6inletdec=ify=((y/2)*2)then60else40inletoffset=match(-1*y)with0->-2|1->-1|2->-1|3->0|4->-1|_->12inletx=(xx+dec)/virtual_case_size-3+offsetin(-1*y,x)(* line_number_to_aff : int -> int*int *)(* convert a line number into a polition on the virtual table serving *)(* for drawing *)(* the coordinate returned corresponds to the final case for the line *)letline_number_to_affn=matchnwith0->(2,1)|1->(1,2)|2->(0,3)|3->(-1,4)|4->(0,5)|5->(5,0)|6->(7,0)|7->(8,1)|8->(9,2)|9->(10,3)|10->(3,6)|11->(5,6)|12->(7,6)|13->(9,6)|14->(10,5)|_->failwith"line"(*raise Rep.Out_of_bounds*)(* draw_lines_won : game -> unit *)(* position a marker indicating the player which has taken the line *)(* this is done for all lines *)letdrawbli=matchlwithNone->failwith"draw"|Mj->letpos=line_number_to_affiin(* print_string "''''";print_int i;print_string "---";Printf.printf "%d,%d\n" (fst pos) (snd pos);*)Graphics.set_color(ifjthencBlackelsecRed);Graphics.fill_rect((fstpos)*30+virtual_table_xoffset-bounds)(height-((sndpos)*55+25)-60)2040letdraw_lines_wonomnm=fori=0to14doifom.(i)<>nm.(i)thendrawbnm.(i)idone(*********************let black_lines = Rep.lines_won_by_player mat Rep.Noir andred_lines = Rep.lines_won_by_player mat Rep.Rougeinprint_string "black : "; print_int (Rep.list_size black_lines);print_newline () ;print_string "red : "; print_int (Rep.list_size red_lines);print_newline() ;let rec draw l col =match l with[] -> ()| h::t -> let pos = line_number_to_aff h inGraphics.set_color col ;Graphics.fill_rect ((fst pos)*30 + virtual_table_xoffset-bounds)(height - ((snd pos)*55 + 25)-60) 20 40 ;draw t colin draw black_lines cBlack ;draw red_lines cRed***************************************************)(* draw_poss : item list -> int -> unit *)(* draw the pieces available for a player based on a list *)(* the parameter "off" indicates the position at which to place the list *)letdraw_possplayerlstoff=letc=ref(1)inletrecdrawl=matchlwith[]->()|v::t->ifplayerthenGraphics.set_colorcBlackelseGraphics.set_colorcRed;letx=offandy=0+(!c)*50inGraphics.fill_circlexybrightness;Graphics.set_colorcWhite;Graphics.moveto(x-3)(y-3);Graphics.draw_string(string_of_intv);c:=!c+1;drawtindraw(List.map(functionPx->x)lst)(* draw_choice : game -> unit *)(* draw the list of pieces still available for each player *)letdraw_choice(J(ca,ma,r1,r2))=Graphics.set_colorcBlue;Graphics.fill_rect(choice_black_offset-30)1060(height-(top_offset+bounds));Graphics.fill_rect(choice_red_offset-30)1060(height-(top_offset+bounds));draw_posstruer1choice_black_offset;draw_possfalser2choice_red_offset(* wait_click : unit -> unit *)(* wait for a mouse click *)letwait_click()=Graphics.wait_next_event[Graphics.Button_down](* item list -> item *)(* return, for play, the piece chosen by the user *)letselect_pionplayerlst=letok=reffalseandchoice=ref99andpion=ref(P(-1))inwhilenot!okdoletst=wait_click()inletsize=List.lengthlstinletx=st.Graphics.mouse_xandy=st.Graphics.mouse_yinchoice:=(y+25)/50-1;if!choice<=size&&((player&&x<65)||((notplayer)&&(x>535)))thenok:=trueelseok:=false;if!okthentrypion:=(List.nthlst!choice);Graphics.set_colorcGreen;Graphics.set_line_width2;Graphics.draw_circle(ifplayerthenchoice_black_offsetelsechoice_red_offset)((!choice+1)*50)(brightness+1)with_->ok:=false;done;!pion(* choiceH : game -> move *)(* return a move for the human player.return the choice of the number, the case, and the piece *)letrecchoiceplayergame=matchgamewith(J(ca,ma,r1,r2))->letchoice=ref(P(-1))andc=ref(-1,P(-1))inletlcl=legal_movesplayergameinwhilenot(List.mem!clcl)doprint_newline();print_string"CHOICE";List.iter(fun(c,Pp)->print_string"[";print_intc;print_string" ";print_intp;print_string"]")(legal_movesplayergame);draw_choicegame;choice:=select_pionplayer(ifplayerthenr1elser2);(* print_string "choice "; print_piece !choice;*)c:=(corresp2(conv(wait_click())),!choice)(* let (x,y) = !c in(print_string "...";print_int x; print_string " "; print_piece y;print_string " -> ";print_string "END_CHOICE";print_newline())*)done;!c(* case, piece *)(* home : unit -> unit *)(* place a message about the game *)lethome()=Graphics.open_graph(" "^(string_of_int(width+10))^"x"^(string_of_int(height+10))^"+50+50");Graphics.moveto(height/2)(width/2);Graphics.set_colorcBlue;Graphics.draw_string"Stonehenge";Graphics.set_colorcBlack;Graphics.moveto22;Graphics.draw_string"Mixte Projets Maîtrise & DESS GLA";wait_click();Graphics.clear_graph()(* exit : unit -> unit *)(* close everything ! *)letexit()=Graphics.close_graph()(* draw_button : int -> int -> int -> int -> string -> unit *)(* draw a button with a message *)letdraw_buttonxywhs=Graphics.set_line_width1;Graphics.set_colorcBlack;Graphics.movetoxy;Graphics.linetox(y+h);Graphics.lineto(x+w)(y+h);Graphics.lineto(x+w)y;Graphics.linetoxy;Graphics.moveto(x+bounds)(height-(top_offset/2));Graphics.draw_strings(* draw_message : string -> unit *)(* position a message *)letdraw_messages=Graphics.set_colorcBlack;Graphics.moveto3(height-(top_offset/2));Graphics.draw_strings(* erase_message : unit -> unit *)(* as the name indicates *)leterase_message()=Graphics.set_colorGraphics.white;Graphics.fill_rect0(height-top_offset+bounds)widthtop_offset(* question : string -> bool *)(* pose the user a question, and wait for a yes/no response *)letquestions=letxb1=(width/2)andxb2=(width/2+30)andwb=25andhb=16andyb=height-20inletrecattente()=lete=wait_click()inif(e.Graphics.mouse_y<(yb+hb))&(e.Graphics.mouse_y>yb)thenif(e.Graphics.mouse_x>xb1)&(e.Graphics.mouse_x<(xb1+wb))thentrueelseif(e.Graphics.mouse_x>xb2)&(e.Graphics.mouse_x<(xb2+wb))thenfalseelseattente()elseattente()indraw_messages;draw_buttonxb1ybwbhb"yes";draw_buttonxb2ybwbhb"no";attente()(* q_begin : unit -> bool *)(* Ask if the player wishes to be the first player or not *)letq_begin()=letb=question"Would you like to play first ?"inerase_message();b(* q_continue : unit -> bool *)(* Ask if the user wishes to play the game again *)letq_continue()=letb=question"Play again ?"inerase_message();b(* won : unit -> unit *)(* a message indicating the machine has won *)letwon()=draw_message"I won :-)";wait_click();erase_message()(* lost : unit -> unit *)(* a message indicating the machine has lost *)letlost()=draw_message"You won :-(";wait_click();erase_message()(* nil : unit -> unit *)(* a message indicating stalemate *)letnil()=draw_message"Stalemate";wait_click();erase_message()(* init : unit -> unit *)(* draw the initial game board *)letinit()=letgame=game_start()indraw_table();draw_choicegame(* drawH : move -> game -> unit *)(* draw a piece for the human player *)(* let drawH cp j = draw_piece cp cBlack ;draw_lines_won j*)(* drawM : move -> game -> unit *)(* draw a piece for the machine player *)(* let drawM cp j = draw_piece cp cRed ;draw_lines_won j*)letprint_placementm=matchmwithNone->print_string"None "|Mj->print_string("Pl "^(ifjthen"1 "else"2 "))letpositionplayermove(J(ca1,m1,r11,r12))(J(ca2,m2,r21,r22)asnew_game)=draw_pieceplayermove;draw_choicenew_game;(* print_string "_______OLD___________________\n";Array.iter print_placement m1; print_newline();List.iter print_piece r11; print_newline();List.iter print_piece r12; print_newline();print_string "_______NEW___________________\n";Array.iter print_placement m2; print_newline();List.iter print_piece r21; print_newline();List.iter print_piece r22; print_newline();*)draw_lines_wonm1m2(*if player then draw_piece move cBlackelse draw_piece move cRed*)letq_player()=letb=question"Is there a machine playing?"inerase_message();bend;;Characters 11114-11127:Warning: this expression should have type unit.Characters 13197-13209:Warning: this expression should have type unit.Characters 13345-13357:Warning: this expression should have type unit.Characters 13478-13490:Warning: this expression should have type unit.module Stone_graph :sigtype piece = Stone_rep.pieceand placement = Stone_rep.placementand case = Stone_rep.caseand game = Stone_rep.gameand move = Stone_rep.moveval brightness : intval cBlack : Graphics.colorval cRed : Graphics.colorval cYellow : Graphics.colorval cGreen : Graphics.colorval cWhite : Graphics.colorval cGray : Graphics.colorval cBlue : Graphics.colorval width : intval height : intval top_offset : intval bounds : intval virtual_table_xoffset : intval choice_black_offset : intval choice_red_offset : intval virtual_case_size : intval corresp : int -> int * intval corresp2 : int * int -> intval col : intval lig : intval draw_background : unit -> unitval draw_places : unit -> unitval draw_force_lines : unit -> unitval draw_final_places : unit -> unitval draw_table : unit -> unitval draw_piece : bool -> int * Stone_rep.piece -> unitval conv : Graphics.status -> int * intval line_number_to_aff : int -> int * intval drawb : Stone_rep.placement -> int -> unitval draw_lines_won :Stone_rep.placement array -> Stone_rep.placement array -> unitval draw_poss : bool -> Stone_rep.piece list -> int -> unitval draw_choice : Stone_rep.game -> unitval wait_click : unit -> Graphics.statusval select_pion : bool -> Stone_rep.piece list -> Stone_rep.pieceval choice : bool -> Stone_rep.game -> int * Stone_rep.pieceval home : unit -> unitval exit : unit -> unitval draw_button : int -> int -> int -> int -> string -> unitval draw_message : string -> unitval erase_message : unit -> unitval question : string -> boolval q_begin : unit -> boolval q_continue : unit -> boolval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval init : unit -> unitval print_placement : Stone_rep.placement -> unitval position :bool ->int * Stone_rep.piece -> Stone_rep.game -> Stone_rep.game -> unitval q_player : unit -> boolend
# moduleStone_skeletonG=FSkeleton(Stone_rep)(Stone_graph)(Stone_eval)(FAlphabeta(Stone_rep)(Stone_eval));;module Stone_skeletonG :sigval depth : int refexception Wonexception Lostexception Nilval won : unit -> unitval lost : unit -> unitval nil : unit -> unitval again : unit -> boolval play_game : Stone_graph.game refval exit : unit -> unitval home : unit -> unitval playH : bool -> unit -> unitval playM : bool -> unit -> unitval init : unit -> (unit -> unit) * (unit -> unit)end
# moduleStone_mainG=FMain(Stone_skeletonG);;module Stone_mainG :sigval play_game : (unit -> 'a) * (unit -> 'b) -> unitval main : unit -> unitend


