Exercises
Polar coordinates
Coordinates as used in the library Graphics are Cartesian. There
a line segment is represented by its starting point (x0,y0)
and its end point (x1,y1). It can be useful to use polar
coordinates instead. Here a line segment is described by its point of
origin (x0,y0), a length (radius) (r) and an angle
(a). The relation between Cartesian and Polar coordinates is
defined by the following equations:
|
|
ì
í
î |
|
| x1 |
= |
x0 + r * cos(a) |
| y1 |
= |
y0 + r * sin(a) |
|
|
# type seg_pol = {x:float; y:float; r:float; a:float};;
type seg_pol = { x: float; y: float; r: float; a: float }
-
Write the function to_cart
that converts polar coordinates to Cartesian ones.
# let to_cart p =
(p.x,p.y),(p.x +. p.r *. (cos p.a), p.y +. p.r *. (sin p.a)) ;;
val to_cart : seg_pol -> (float * float) * (float * float) = <fun>
- Write the function draw_seg which
displays a line segment defined by polar coordinates in the reference
point of Graphics.
# let draw_seg p =
let (x1,y1),(x2,y2) = to_cart p in
Graphics.moveto (int_of_float x1) (int_of_float y1);
Graphics.lineto (int_of_float x2) (int_of_float y2) ;;
val draw_seg : seg_pol -> unit = <fun>
- One of the motivations behind polar coordinates is to be able
to easily apply transformations to line segments. A translation only
modifies the point of origin, a rotation only affects the angle field
and modifying the scale only changes the length field. Generally,
one can represent a transformation as a triple of floats: the first
represents the translation (we do not consider the case of translating
the second point of the line segment here), the second the rotation and
the third the scaling factor. Define the function
app_trans
which takes a line segment in polar coordinates and
a triple of transformations and returns the new segment.
# let app_trans seg ( da, dr, dxy ) =
let _,(x1,y1) = to_cart {seg with r = seg.r *. dxy} in
{x=x1; y=y1; a=seg.a +. da; r=seg.r *. dr} ;;
val app_trans : seg_pol -> float * float * float -> seg_pol = <fun>
- One can construct recursive drawings by iterating
transformations. Write the function draw_r
which takes as arguments a line segment s, a number of
iterations n, a list of transformations and displays all the
segments resulting from the transformations on s iterated up
to n.
# let rec draw_r s n l =
if n = 0 then ()
else
begin
draw_seg s;
List.iter (fun t -> draw_r (app_trans s t) (n-1) l) l
end ;;
val draw_r : seg_pol -> int -> (float * float * float) list -> unit = <fun>
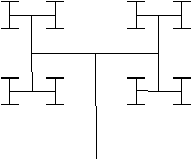
- Verify that the following program does produce
the images in figure 5.10.
let pi = 3.1415927 ;;
let s = {x=100.; y= 0.; a= pi /. 2.; r = 100.} ;;
draw_r s 6 [ (-.pi/.2.),0.6,1.; (pi/.2.), 0.6,1.0] ;;
Graphics.clear_graph();;
draw_r s 6 [(-.pi /. 6.), 0.6, 0.766;
(-.pi /. 4.), 0.55, 0.333;
(pi /. 3.), 0.4, 0.5 ] ;;
# Graphics.close_graph();;
- : unit = ()
# Graphics.open_graph " 200x200";;
- : unit = ()
# let pi = 3.1415927 ;;
val pi : float = 3.1415927
# let s = {x=100.; y= 0.; a= pi /. 2.; r = 100.} ;;
val s : seg_pol = {x=100; y=0; r=100; a=1.57079635}
# draw_r s 6 [ (-.pi/.2.),0.6,1.; (pi/.2.), 0.6,1.0] ;;
- : unit = ()
# Graphics.clear_graph();;
- : unit = ()
# draw_r s 6 [(-.pi /. 6.), 0.6, 0.766;
(-.pi /. 4.), 0.55, 0.333;
(pi /. 3.), 0.4, 0.5 ] ;;
- : unit = ()
Figure 5.10: Recursive drawings.
Bitmap editor
We will attempt to write a small bitmap editor (similar to the command
bitmap in X-window). For this we represent a bitmap by its
dimensions (width and height), the pixel size and a two-dimensional
table of booleans.
-
Define a type bitmap_state describing
the information necessary for containing the values of the pixels,
the size of the bitmap and the colors of displayed and erased points.
# type bitmap_state =
{w : int; h : int; fg : Graphics.color; bg : Graphics.color;
pix : bool array array; s : int} ;;
type bitmap_state =
{ w: int;
h: int;
fg: Graphics.color;
bg: Graphics.color;
pix: bool array array;
s: int }
- Write a function for creating bitmaps
(create_bitmap)
and for displaying bitmaps
(draw_bitmap) .
# let create_bitmap x y f g s =
let r = Array.make_matrix x y false in
{ w = x; h = y; fg = f; bg = g; pix = r; s = s} ;;
val create_bitmap :
int -> int -> Graphics.color -> Graphics.color -> int -> bitmap_state =
<fun>
# let draw_pix i j s c =
Graphics.set_color c;
Graphics.fill_rect (i*s+1) (j*s+1) (s-1) (s-1) ;;
val draw_pix : int -> int -> int -> Graphics.color -> unit = <fun>
# let draw_bitmap b =
for i=0 to b.w-1 do
for j=0 to b.h-1 do
draw_pix i j b.s (if b.pix.(i).(j) then b.fg else b.bg)
done
done ;;
val draw_bitmap : bitmap_state -> unit = <fun>
- Write the functions read_bitmap
and write_bitmap which respectively read
and write in a file passed as parameter following the ASCII format of
X-window. If the file does not exist, the function for reading creates
a new bitmap using the function create_bitmap.
# let read_file filename =
let ic = open_in filename in
let rec aux () =
try
let line = (input_line ic) in
line :: (aux ())
with End_of_file -> close_in ic ; []
in aux ();;
val read_file : string -> string list = <fun>
# let read_bitmap filename =
let r = Array.of_list (read_file filename) in
let h = Array.length r in
let w = String.length r.(0) in
let b = create_bitmap w h Graphics.black Graphics.white 10 in
for j = 0 to h - 1 do
for i = 0 to w - 1 do
b.pix.(i).(j) <- ( r.(j).[i] = '#')
done
done;
b ;;
val read_bitmap : string -> bitmap_state = <fun>
# let write_bitmap filename b =
let oc = open_out filename in
let f x = output_char oc (if x then '#' else '-') in
Array.iter (fun x -> (Array.iter f x); output_char oc '\n') b.pix ;
close_out oc ;;
val write_bitmap : string -> bitmap_state -> unit = <fun>
A displayed pixel is represented by the character #, the absence
of a pixel by the character -. Each line of characters represents
a line of the bitmap. One can test the program using the functions
atobm and bmtoa of X-window, which convert between
this ASCII format and the format of bitmaps created by the command
bitmap. Here is an example.
###################-------------#######---------######
###################---------------###-------------##--
###-----###-----###---------------###-------------#---
##------###------##----------------###-----------##---
#-------###-------#-----------------###---------##----
#-------###-------#-----------------###--------##-----
--------###--------------------------###-------#------
--------###-------###############-----###----##-------
--------###-------###---------###------###--##--------
--------###-------###----------##-------###-#---------
--------###-------###-----------#-------#####---------
--------###-------###-----------#--------###----------
--------###-------###--------------------####---------
--------###-------###--------------------####---------
--------###-------###------#-----------##---###-------
--------###-------###------#----------##----###-------
--------###-------##########----------#------###------
--------###-------##########---------##-------###-----
--------###-------###------#--------##--------###-----
--------###-------###------#-------##----------###----
--------###-------###--------------#------------###---
------#######-----###-----------#######--------#######
------------------###---------------------------------
------------------###-----------#---------------------
------------------###-----------#---------------------
------------------###----------##---------------------
------------------###---------###---------------------
------------------###############---------------------
- We reuse the skeleton for interactive loops
on page ?? to construct the graphical interface
of the editor. The human-computer interface is very simple. The bitmap
is permanently displayed in the graphical window. A mouse click in one
of the slots of the bitmap inverts its color. This change is reflected
on the screen. Pressing the key 'S' saves the bitmap in a file. The key
'Q' terminates the program.
-
Write a function start of type
bitmap_state -> unit -> unit which opens a graphical window
and displays the bitmap passed as parameter.
# exception End ;;
exception End
# let skel f_init f_end f_key f_mouse f_except =
f_init ();
try
while true do
try
let s = Graphics.wait_next_event
[Graphics.Button_down; Graphics.Key_pressed] in
if s.Graphics.keypressed
then f_key s.Graphics.key
else if s.Graphics.button
then f_mouse s.Graphics.mouse_x s.Graphics.mouse_y
with
End -> raise End
| e -> f_except e
done
with
End -> f_end () ;;
val skel :
(unit -> 'a) ->
(unit -> unit) ->
(char -> unit) -> (int -> int -> unit) -> (exn -> unit) -> unit = <fun>
# let start b () =
let sw = 1+b.w*b.s and sh = 1+b.h*b.s in
Graphics.open_graph (" " ^ (string_of_int sw) ^ "x" ^ (string_of_int sh)) ;
Graphics.set_color (Graphics.rgb 150 150 150) ;
Graphics.fill_rect 0 0 sw sh ;
draw_bitmap b ;;
val start : bitmap_state -> unit -> unit = <fun>
- Write a function stop that closes the
graphical window and exits the program.
# let stop () = Graphics.close_graph() ; exit 0 ;;
val stop : unit -> 'a = <fun>
- Write a function mouse of type
bitmap_state -> int -> int -> unit which modifies the pixel
state corresponding to the mouse click and displays the change.
# let mouse b x y =
let i,j = (x / b.s),(y/b.s) in
if ( i < b.w ) && ( j < b.h) then
begin
b.pix.(i).(j) <- not b.pix.(i).(j) ;
draw_pix i j b.s (if b.pix.(i).(j) then b.fg else b.bg)
end ;;
val mouse : bitmap_state -> int -> int -> unit = <fun>
- Write a function key of type string
-> bitmap_state -> char -> unit which takes as arguments the name
of a file, a bitmap and the char of the pressed key and executes the
associated actions: saving to a file for the key 'S' and raising of the
exception End for the key 'Q'.
# let key filename b c =
match c with
'q' | 'Q' -> raise End
| 's' | 'S' -> write_bitmap filename b
| _ -> () ;;
val key : string -> bitmap_state -> char -> unit = <fun>
- Write a function go which takes the name
of a file as parameter, loads the bitmap, displays it and starts the
interactive loop.
# let go name =
let b = try
read_bitmap name
with
_ -> create_bitmap 10 10 Graphics.black Graphics.white 10
in skel (start b) stop (key name b) (mouse b) (fun e -> ()) ;;
val go : string -> unit = <fun>
Earth worm
The earth worm is a small, longish organism of a certain size which grows
over time while eating objects in a world. The earth worm moves constantly
in one direction. The only actions allowing a player to control it are
changes in direction. The earth worm vanishes if it touches a border
of the world or if it passes over a part of its body. It is most often
represented by a vector of coordinates with two principal indices:
its head and its tail. A move will therefore be computed from the new
coordinates of its head, will display it and erase the tail. A growth
step only modifies its head without affecting the tail of the earth worm.
-
Write the Objective CAML type or types for
representing an earth worm and the world where it evolves. One can
represent an earth worm by a queue of its coordinates.
# type cell = Empty | Full ;;
type cell = | Empty | Full
# type world = { sx : int; sy : int; cells : cell array array } ;;
type world = { sx: int; sy: int; cells: cell array array }
# type worm = { mutable head : int; mutable queue : int; mutable size : int;
mutable vx : int; mutable vy : int;
pos : (int * int) array } ;;
type worm =
{ mutable head: int;
mutable queue: int;
mutable size: int;
mutable vx: int;
mutable vy: int;
pos: (int * int) array }
# type game = { w : world; wo : worm; s_cell : int;
fg : Graphics.color; bg : Graphics.color } ;;
type game =
{ w: world;
wo: worm;
s_cell: int;
fg: Graphics.color;
bg: Graphics.color }
- Write a function for initialization
and displaying an earth worm in a world.
# let init_world sx sy =
{ sx = sx; sy = sy; cells = Array.create_matrix sx sy Empty } ;;
val init_world : int -> int -> world = <fun>
# let init_worm s s_max x =
if s > x then failwith "init_worm"
else
begin
let wo = { head = s-1; queue = 0; size = s; vx = 1; vy = 0;
pos = Array.create s_max (0,0) } in
let y = x / 2
and rx = ref (x/2 - s/2) in
for i=0 to s-1 do wo.pos.(i) <- (!rx,y) ; incr rx done ;
wo
end ;;
val init_worm : int -> int -> int -> worm = <fun>
# let init_game s s_max sx sy sc c1 c2 =
let j = { w = init_world sx sy; wo = init_worm s s_max sx;
s_cell = sc; fg = c1; bg = c2 } in
for i=j.wo.head to j.wo.queue do
let (x,y) = j.wo.pos.(i) in
j.w.cells.(x).(y) <- Full
done ;
j ;;
val init_game :
int -> int -> int -> int -> int -> Graphics.color -> Graphics.color -> game =
<fun>
# let display_cell x y s c =
Graphics.set_color c;
Graphics.fill_rect (x*s) (y*s) s s ;;
val display_cell : int -> int -> int -> Graphics.color -> unit = <fun>
# let display_world game =
let w = game.w in
for i=0 to w.sx-1 do
for j=0 to w.sy-1 do
let col = if w.cells.(i).(j) = Full then game.fg else game.bg in
display_cell i j game.s_cell col
done
done ;;
val display_world : game -> unit = <fun>
- Modify the function skel of the
skeleton of the program which causes an action at each execution of the
interactive loop, parameterized by a function. The treatment of keyboard
events must not block.
(************** interaction **********)
# let tempo ti =
for i = 0 to ti do ignore (i * ti * ti ) done ;;
val tempo : int -> unit = <fun>
# exception End;;
exception End
# let skel f_init f_end f_key f_mouse f_except f_run =
f_init ();
try
while true do
try
tempo 200000 ;
if Graphics.key_pressed() then f_key (Graphics.read_key()) ;
f_run ()
with
End -> raise End
| e -> f_except e
done
with
End -> f_end () ;;
val skel :
(unit -> 'a) ->
(unit -> unit) ->
(char -> unit) -> 'b -> (exn -> 'c) -> (unit -> 'c) -> unit = <fun>
- Write a function run which
advances the earth worm in the game. This function raises the exception
Victory (if the worm reaches a certain size) and Loss
if it hits a full slot or a border of the world.
# exception Loss;;
exception Loss
# exception Victory;;
exception Victory
# let run game temps itemps () =
incr temps;
let wo = game.wo in
let s = Array.length wo.pos in
let sx,sy = wo.pos.(wo.head) in
let nx,ny = sx+wo.vx,sy+wo.vy in
if (nx < 0 ) || (nx >= game.w.sx) || (ny < 0) || (ny >= game.w.sy)
then raise Loss
else if game.w.cells.(nx).(ny) = Full then raise Loss
else if wo.head = wo.queue then raise Victory
else
begin
let nhead = (wo.head + 1) mod s in
wo.head <- nhead ;
wo.pos.(wo.head) <- (nx,ny);
game.w.cells.(nx).(ny) <- Full ;
display_cell nx ny game.s_cell game.fg ;
if (!temps mod !itemps < (!itemps - 2)) then
begin
let qx,qy = wo.pos.(wo.queue) in
game.w.cells.(qx).(qy) <- Empty ;
display_cell qx qy game.s_cell game.bg ;
wo.queue <- (wo.queue + 1) mod s
end
end ;;
val run : game -> int ref -> int ref -> unit -> unit = <fun>
- Write a function for keyboard interaction
which modifies the direction of the earth worm.
# let key lact game c =
match c with
'q' | 'Q' -> raise End
| 'p' | 'P' -> ignore (Graphics.read_key ())
| '2' | '4' | '6' | '8' ->
let dx,dy = List.assoc c lact in
game.wo.vx <- dx ;
game.wo.vy <- dy
| _ -> () ;;
val key : (char * (int * int)) list -> game -> char -> unit = <fun>
- Write the other utility functions for handling
interaction and pass them to the new skeleton of the program.
# let start game () =
let sw = game.s_cell * game.w.sx and sh = game.s_cell * game.w.sy in
let size = (string_of_int sw) ^ "x" ^ (string_of_int sh) in
Graphics.open_graph (" " ^ size) ;
Graphics.set_color (Graphics.rgb 150 150 150);
Graphics.fill_rect 0 0 sw sh;
display_world game;
ignore (Graphics.read_key()) ;;
val start : game -> unit -> unit = <fun>
# let stop game () =
ignore (Graphics.read_key());
Graphics.close_graph() ;;
val stop : 'a -> unit -> unit = <fun>
# let mouse x y = () ;;
val mouse : 'a -> 'b -> unit = <fun>
# let except e = match e with
Loss -> print_endline "LOSS"; raise End
| Victory -> print_endline "VICTORY"; raise End
| e -> raise e ;;
val except : exn -> 'a = <fun>
- Write the initiating function which starts
the application.
# let la = [ ('2',(0,-1)) ; ('4',(-1,0)) ; ('6',(1,0)) ; ('8',(0,1)) ] ;;
val la : (char * (int * int)) list =
['2', (0, -1); '4', (-1, 0); '6', (1, 0); '8', (0, ...)]
# let go x y sc =
let col = Graphics.rgb 150 150 150 in
let game = init_game 5 (x*y /2) x y sc Graphics.black col in
skel (start game) (stop game) (key la game) mouse except (run game (ref 0) (ref 100));;
val go : int -> int -> int -> unit = <fun>