Types and Genericity
Besides the ability to model a problem using aggregation and inheritance
relations, object-oriented programming is interesting because it provides the ability
to reuse or modify the behavior of classes. However, extending an Objective CAML
class must preserve the static typing properties of the language.
With abstract classes, you can factorize code and group their
subclasses into one
``communication protocol''. An abstract class fixes the
names and types of messages that may be received by instances of
child classes. This technique will be better appreciated in
connection with multiple inheritance.
The notion of an open object type (or simply an open type) that
specifies the required methods allows code to work with instances using generic
functions. But you may need to make the type constraints precise; this will be
necessary for parameterized classes, which provide the genericity of
parameterized polymorphism in the context of classes. With this latter
object layer feature, Objective CAML can really be generic.
Abstract Classes and Methods
In abstract classes, some methods are declared without a body. Such
methods are called abstract. It is illegal to instantiate an abstract
class; new cannot be used. The keyword virtual is used to
indicate that a class or method is abstract.
Syntax
class virtual name =
object ...end
A class must be declared abstract as soon as one of its methods is
abstract. A method is declared abstract by providing only the method type.
Syntax
method virtual name : type
When a subclass of an abstract class redefines all of the abstract
methods of its parent, then it may become concrete; otherwise it also has to
be declared abstract.
As an example, suppose we want to construct a set of displayable objects, all with a method
print that will display the object's contents translated into a
character string. All such objects need a method
to_string. We define class printable.
The string may vary according to the nature of the objects that we consider;
therefore method to_string is abstract in the declaration of
printable and consequently the class is also abstract.
# class virtual printable () =
object(self)
method virtual to_string : unit -> string
method print () = print_string (self#to_string())
end ;;
class virtual printable :
unit ->
object
method print : unit -> unit
method virtual to_string : unit -> string
end
We note that the abstractness of the class and of its method
to_string is made clear in the type we obtain.
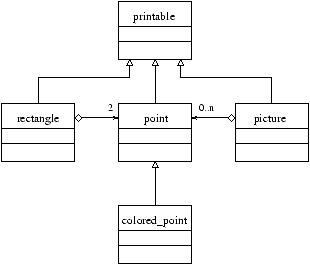
From this class, let us try to define the class hierarchy of figure 15.4.
Figure 15.4: Relations between classes of displayable objects.
It is easy to redefine the classes point, colored_point and
picture by adding to their declarations a line inherit
printable () that provides them with a method print through inheritance.
# let p = new point (1,1) in p#print() ;;
( 1, 1)- : unit = ()
# let pc = new colored_point (2,2) "blue" in pc#print() ;;
( 2, 2) with color blue- : unit = ()
# let t = new picture 3 in t#add (new point (1,1)) ;
t#add (new point (3,2)) ;
t#add (new point (1,4)) ;
t#print() ;;
[ ( 1, 1) ( 3, 2) ( 1, 4)]- : unit = ()
Subclass rectangle below inherits from printable, and defines
method to_string. Instance variables llc (resp. urc)
mean the lower left corner point (resp. upper right corner point) in the rectangle.
# class rectangle (p1,p2) =
object
inherit printable ()
val llc = (p1 : point)
val urc = (p2 : point)
method to_string () = "[" ^ llc#to_string() ^ "," ^ urc#to_string() ^ "]"
end ;;
class rectangle :
point * point ->
object
val llc : point
val urc : point
method print : unit -> unit
method to_string : unit -> string
end
Class rectangle inherits from the abstract class printable,
and thus receives method print. It has two instance variables of type
point: the lower left corner (llc) and upper right corner.
Method to_string sends the message to_string to
its point instance variables llc and urc.
# let r = new rectangle (new point (2,3), new point (4,5));;
val r : rectangle = <obj>
# r#print();;
[( 2, 3),( 4, 5)]- : unit = ()
Classes, Types, and Objects
You may remember that the type of an object is determined by the type of its
methods. For instance, the type point, inferred during the declaration of
class point, is an abbreviation for type:
point =
< distance : unit -> float; get_x : int; get_y : int;
moveto : int * int -> unit; rmoveto : int * int -> unit;
to_string : unit -> string >
This is a closed type; that is, all methods and associated types are fixed.
No additional methods and types are allowed. Upon a class declaration, the mechanism of type
inference computes the closed type associated with class.
Open Types
Since sending a message to an object is part of the language, you may
define a function that sends a message to an object whose type is still undefined.
# let f x = x#get_x ;;
val f : < get_x : 'a; .. > -> 'a = <fun>
The type inferred for the argument of f is an object type, since a
message is sent to x, but this object type is open. In
function f, parameter x must have at least a method
get_x. Since the result of sending this message is not used within
function f, its type has to be as general as possible (i.e. a variable
of type 'a). So type inference allows the function
f to be used with any object having a method get_x.
The double points (..) at the end of the type < get_x : 'a; .. >
indicate that the type of x is open.
# f (new point(2,3)) ;;
- : int = 2
# f (new colored_point(2,3) "emerald") ;;
- : int = 2
# class c () =
object
method get_x = "I have a method get_x"
end ;;
class c : unit -> object method get_x : string end
# f (new c ()) ;;
- : string = "I have a method get_x"
Type inference for classes may generate open types, particularly for initial
values in instance construction. The following example constructs a class
couple, whose initial values a and b have a method
to_string.
# class couple (a,b) =
object
val p0 = a
val p1 = b
method to_string() = p0#to_string() ^ p1#to_string()
method copy () = new couple (p0,p1)
end ;;
class couple :
(< to_string : unit -> string; .. > as 'a) *
(< to_string : unit -> string; .. > as 'b) ->
object
val p0 : 'a
val p1 : 'b
method copy : unit -> couple
method to_string : unit -> string
end
The types of both a and b are open types, with method
to_string. We note that these two types are considered to be
different.
They are marked ``as 'a'' and ``as 'b'', respectively. Variables of
types 'a and 'b are constrained by the generated type.
We use the sharp symbol to indicate the open type built from a closed type
obj_type:
Syntax
#obj_type
The type obtained contains all of the methods of type obj_type and
terminates with a double point.
Type Constraints.
In the chapter on functional programming (see page ??), we
showed how an expression can be constrained to have a type more precise
than what is produced by inference. Object types (open or closed) can be used to
enhance such constraints. One may want to open a priori the type of a
defined object, in order to apply it to a forthcoming method. We can use an
open object constraint:
Syntax
(name:#type)
Which allows us to write:
# let g (x : #point) = x#message;;
val g :
< distance : unit -> float; get_x : int; get_y : int; message : 'a;
moveto : int * int -> unit; print : unit -> unit;
rmoveto : int * int -> unit; to_string : unit -> string; .. > ->
'a = <fun>
The type constraint with #point forces x to have at
least all of the methods of point, and sending message
``message'' adds a method to the type of parameter x.
Just as in the rest of the language, the object extension of Objective CAML provides
static typing through inference. When this mechanism does not have enough
information to determine the type of an expression, a type variable is
assigned. We have just seen that this process is also valid for typing objects;
however, it sometimes leads to ambiguous situations which the user must
resolve by explicitly giving type information.
# class a_point p0 =
object
val p = p0
method to_string() = p#to_string()
end ;;
Characters 6-89:
Some type variables are unbound in this type:
class a_point :
(< to_string : unit -> 'b; .. > as 'a) ->
object val p : 'a method to_string : unit -> 'b end
The method to_string has type unit -> 'a where 'a is unbound
We resolve this ambiguity by saying that parameter p0 has type #point.
# class a_point (p0 : #point) =
object
val p = p0
method to_string() = p#to_string()
end ;;
class a_point :
(#point as 'a) -> object val p : 'a method to_string : unit -> string end
In order to set type constraints in several places in a class declaration, the
following syntax is used:
Syntax
constraint type1 = type2
The above example can be written specifying that parameter p0 has type
'a, then putting a type constraint upon variable 'a.
# class a_point (p0 : 'a) =
object
constraint 'a = #point
val p = p0
method to_string() = p#to_string()
end ;;
class a_point :
(#point as 'a) -> object val p : 'a method to_string : unit -> string end
Several type constraints can be given in a class declaration.
Warning
An open type cannot appear as the type of a method.
This strong restriction exists because an open type contains an
uninstantiated type variable coming from the rest of the type. Since one cannot
have a free variable type in a type declaration, a method containing such
a type is rejected by type inference.
# class b_point p0 =
object
inherit a_point p0
method get = p
end ;;
Characters 6-77:
Some type variables are unbound in this type:
class b_point :
(#point as 'a) ->
object val p : 'a method get : 'a method to_string : unit -> string end
The method get has type #point where .. is unbound
In fact, due to the constraint ``constraint 'a = #point'', the type of
get is the open type #point. The latter contains a free
variable type noted by a double point (..), which is not allowed.
Inheritance and the Type of self
There exists an exception to the prohibition of a type variable in the type of
methods: a variable may stand for the type of the object itself
(self). Consider a method testing the equality
between two points.
# class point_eq (x,y) =
object (self : 'a)
inherit point (x,y)
method eq (p:'a) = (self#get_x = p#get_x) && (self#get_y = p#get_y)
end ;;
class point_eq :
int * int ->
object ('a)
val mutable x : int
val mutable y : int
method distance : unit -> float
method eq : 'a -> bool
method get_x : int
method get_y : int
method moveto : int * int -> unit
method print : unit -> unit
method rmoveto : int * int -> unit
method to_string : unit -> string
end
The type of method eq is 'a -> bool, but the type variable
stands for the type of the instance at construction time.
You can inherit from the class point_eq and redefine the method eq,
whose type is still parameterized by the instance type.
# class colored_point_eq (xc,yc) c =
object (self : 'a)
inherit point_eq (xc,yc) as super
val c = (c:string)
method get_c = c
method eq (pc : 'a) = (self#get_x = pc#get_x) && (self#get_y = pc#get_y)
&& (self#get_c = pc#get_c)
end ;;
class colored_point_eq :
int * int ->
string ->
object ('a)
val c : string
val mutable x : int
val mutable y : int
method distance : unit -> float
method eq : 'a -> bool
method get_c : string
method get_x : int
method get_y : int
method moveto : int * int -> unit
method print : unit -> unit
method rmoveto : int * int -> unit
method to_string : unit -> string
end
The method eq from class colored_point_eq still has type
'a -> bool; but now the variable 'a stands for the type of an
instance of class colored_point_eq. The definition of eq
in class colored_point_eq masks the inherited one. Methods
containing the type of the instance in their type are called binary methods. They will
cause some limitations in the subtyping relation described in page
??.
Multiple Inheritance
With multiple inheritance, you can inherit data fields and methods from several
classes. When there are identical names for fields or methods, only the last
declaration is kept, according to the order of inheritance
declarations. Nevertheless, it is possible to reference a method of one of the
parent classes by associating different names with the inherited classes.
This is not true for instance variables: if an inherited class masks an
instance variable of a previously inherited class, the latter is no longer
directly accessible. The various inherited classes do not need to have an
inheritance relation. Multiple inheritance is of interest because it increases
class reuse.
Let us define the abstract class geometric_object, which declares two
virtual methods compute_area and compute_peri for
computing the area and perimeter.
# class virtual geometric_object () =
object
method virtual compute_area : unit -> float
method virtual compute_peri : unit -> float
end;;
Then we redefine class rectangle as follows:
# class rectangle_1 ((p1,p2) :'a) =
object
constraint 'a = point * point
inherit printable ()
inherit geometric_object ()
val llc = p1
val urc = p2
method to_string () =
"["^llc#to_string()^","^urc#to_string()^"]"
method compute_area() =
float ( abs(urc#get_x - llc#get_x) * abs(urc#get_y - llc#get_y))
method compute_peri() =
float ( (abs(urc#get_x - llc#get_x) + abs(urc#get_y - llc#get_y)) * 2)
end;;
class rectangle_1 :
point * point ->
object
val llc : point
val urc : point
method compute_area : unit -> float
method compute_peri : unit -> float
method print : unit -> unit
method to_string : unit -> string
end
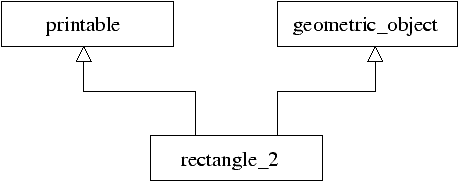
This implementation of classes respects the inheritance graph of figure 15.5.
Figure 15.5: Multiple inheritance.
In order to avoid rewriting the methods of class rectangle, we may
directly inherit from rectangle, as shown in figure 15.6.
Figure 15.6: Multiple inheritance (continued).
In such a case, only the abstract methods of the abstract class
geometric_object must be defined in rectangle_2.
# class rectangle_2 (p2 :'a) =
object
constraint 'a = point * point
inherit rectangle p2
inherit geometric_object ()
method compute_area() =
float ( abs(urc#get_x - llc#get_x) * abs(urc#get_y - llc#get_y))
method compute_peri() =
float ( (abs(urc#get_x - llc#get_x) + abs(urc#get_y - llc#get_y)) * 2)
end;;
Continuing in the same vein, the hierarchies printable and
geometric_object could have been defined separately, until
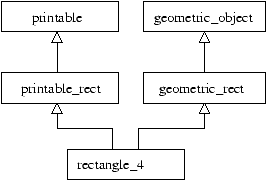
it became useful to have a class with both behaviors. Figure
15.7 displays the relations defined in this way.
Figure 15.7: Multiple inheritance (end).
If we assume that classes printable_rect and
geometric_rect define instance variables for the corners of a
rectangle, we get class rectangle_3 with four points (two per corner).
class rectangle_3 (p1,p2) =
inherit printable_rect (p1,p2) as super_print
inherit geometric_rect (p1,p2) as super_geo
end;;
In the case where methods of the same type exist in both classes
..._rect, then only the last one is visible. However, by naming
parent classes (super_...), it is always possible to invoke a
method from either parent.
Multiple inheritance allows factoring of the code by integrating methods
already written from various parent classes to build new
entities. The price paid is the size of constructed objects, which are bigger
than necessary due to duplicated fields, or inherited fields useless for a given
application. Furthermore, when there is duplication (as in our last
example), communication between these fields must be established manually
(update, etc.). In the last example for class rectangle_3, we obtain
instance variables of classes printable_rect and
geometric_rect. If one of these classes has a method which modifies
these variables (such as a scaling factor), then it is necessary to propagate
these modifications to variables inherited from the other class. Such a heavy
communication between inherited instance variables often signals a poor
modeling of the given problem.
Parameterized Classes
Parameterized classes let Objective CAML's parameterized
polymorphism be used in classes. As with the type declarations of Objective CAML,
class declarations can be parameterized with type variables. This provides new opportunities for
genericity and code reuse. Parameterized classes are integrated with ML-like typing when type
inference produces parameterized types.
The syntax differs slightly from the declaration of parameterized types; type
parameters are between brackets.
Syntax
class ['a, 'b, ...]
name = object ...end
The Objective CAML type is noted as usual:
('a,'b,...) name.
For instance, if a class pair is required, a naive solution would be to set:
# class pair x0 y0 =
object
val x = x0
val y = y0
method fst = x
method snd = y
end ;;
Characters 6-106:
Some type variables are unbound in this type:
class pair :
'a ->
'b -> object val x : 'a val y : 'b method fst : 'a method snd : 'b end
The method fst has type 'a where 'a is unbound
One again gets the typing error mentioned when class a_point was
defined (page ??). The error message says
that type variable 'a, assigned to parameter x0 (and
therefore to x and fst), is not bound.
As in the case of parameterized types, it is necessary to parameterize class
pair with two type variables, and force the type of construction parameters
x0 and y0 to obtain a correct typing:
# class ['a,'b] pair (x0:'a) (y0:'b) =
object
val x = x0
val y = y0
method fst = x
method snd = y
end ;;
class ['a, 'b] pair :
'a ->
'b -> object val x : 'a val y : 'b method fst : 'a method snd : 'b end
Type inference displays a class interface parameterized by variables of type
'a and 'b.
When a value of a parameterized class is constructed, type parameters are
instantiated with the types of the construction parameters:
# let p = new pair 2 'X';;
val p : (int, char) pair = <obj>
# p#fst;;
- : int = 2
# let q = new pair 3.12 true;;
val q : (float, bool) pair = <obj>
# q#snd;;
- : bool = true
Note
In class declarations, type parameters are shown between brackets, but in
types, they are shown between parentheses.
Inheritance of Parameterized Classes
When inheriting from a parameterized class, one has to indicate the parameters
of the class.
Let us define a class acc_pair that inherits from ('a,'b) pair;
we add two methods for accessing the fields,
get1 and get2,
# class ['a,'b] acc_pair (x0 : 'a) (y0 : 'b) =
object
inherit ['a,'b] pair x0 y0
method get1 z = if x = z then y else raise Not_found
method get2 z = if y = z then x else raise Not_found
end;;
class ['a, 'b] acc_pair :
'a ->
'b ->
object
val x : 'a
val y : 'b
method fst : 'a
method get1 : 'a -> 'b
method get2 : 'b -> 'a
method snd : 'b
end
# let p = new acc_pair 3 true;;
val p : (int, bool) acc_pair = <obj>
# p#get1 3;;
- : bool = true
We can make the type parameters of the inherited parameterized class more precise,
e.g. for a pair of points.
# class point_pair (p1,p2) =
object
inherit [point,point] pair p1 p2
end;;
class point_pair :
point * point ->
object
val x : point
val y : point
method fst : point
method snd : point
end
Class point_pair no longer needs type parameters, since parameters
'a and 'b are completely determined.
To build pairs of displayable objects (i.e. having a method print), we
reuse the abstract class printable (see page ??),
then we define the class printable_pair which inherits from pair.
# class printable_pair x0 y0 =
object
inherit [printable, printable] acc_pair x0 y0
method print () = x#print(); y#print ()
end;;
This implementation allows us to construct pairs of instances of
printable, but it cannot be used for objects of another class with a
method print.
We could try to open type printable used as a type parameter for
acc_pair:
# class printable_pair (x0 ) (y0 ) =
object
inherit [ #printable, #printable ] acc_pair x0 y0
method print () = x#print(); y#print ()
end;;
Characters 6-149:
Some type variables are unbound in this type:
class printable_pair :
(#printable as 'a) ->
(#printable as 'b) ->
object
val x : 'a
val y : 'b
method fst : 'a
method get1 : 'a -> 'b
method get2 : 'b -> 'a
method print : unit -> unit
method snd : 'b
end
The method fst has type #printable where .. is unbound
This first attempt fails because methods fst and snd contain
an open type.
So we shall keep the type parameters of the class, while constraining them to
the open type #printable.
# class ['a,'b] printable_pair (x0 ) (y0 ) =
object
constraint 'a = #printable
constraint 'b = #printable
inherit ['a,'b] acc_pair x0 y0
method print () = x#print(); y#print ()
end;;
class ['a, 'b] printable_pair :
'a ->
'b ->
object
constraint 'a = #printable
constraint 'b = #printable
val x : 'a
val y : 'b
method fst : 'a
method get1 : 'a -> 'b
method get2 : 'b -> 'a
method print : unit -> unit
method snd : 'b
end
Then we construct a displayable pair containing a point and a colored point.
# let pp = new printable_pair
(new point (1,2)) (new colored_point (3,4) "green");;
val pp : (point, colored_point) printable_pair = <obj>
# pp#print();;
( 1, 2)( 3, 4) with color green- : unit = ()
Parameterized Classes and Typing
From the point of view of types, a parameterized class is a parameterized
type. A value of such a type can contain weak type variables.
# let r = new pair [] [];;
val r : ('_a list, '_b list) pair = <obj>
# r#fst;;
- : '_a list = []
# r#fst = [1;2];;
- : bool = false
# r;;
- : (int list, '_a list) pair = <obj>
A parameterized class can also be viewed as a closed object type; therefore
nothing prevents us from also using it as an open type with the sharp
notation.
# let compare_nothing ( x : ('a, 'a) #pair) =
if x#fst = x#fst then x#mess else x#mess2;;
val compare_nothing :
< fst : 'a; mess : 'b; mess2 : 'b; snd : 'a; .. > -> 'b = <fun>
This lets us construct parameterized types that contain weak type
variables that are also open object types.
# let prettytype x ( y : ('a, 'a) #pair) = if x = y#fst then y else y;;
val prettytype : 'a -> (('a, 'a) #pair as 'b) -> 'b = <fun>
If this function is applied to one parameter, we get a closure, whose type
variables are weak. An open type, such as #pair, still contains
uninstantiated parts, represented by the double point (..). In this respect,
an open type is a partially known type parameter. Upon weakening
such a type after a partial application, the displayer specifies that the
type variable representing this open type has been weakened. Then the notation
is _#pair.
# let g = prettytype 3;;
val g : ((int, int) _#pair as 'a) -> 'a = <fun>
Now, if function g is applied to a pair, its weak type is modified.
# g (new acc_pair 2 3);;
- : (int, int) acc_pair = <obj>
# g;;
- : (int, int) acc_pair -> (int, int) acc_pair = <fun>
Then we can no longer use g on simple pairs.
# g (new pair 1 1);;
Characters 4-16:
This expression has type (int, int) pair = < fst : int; snd : int >
but is here used with type
(int, int) acc_pair =
< fst : int; get1 : int -> int; get2 : int -> int; snd : int >
Only the second object type has a method get1
Finally, since parameters of the parameterized class can also get weakened, we
obtain the following example.
# let h = prettytype [];;
val h : (('_b list, '_b list) _#pair as 'a) -> 'a = <fun>
# let h2 = h (new pair [] [1;2]);;
val h2 : (int list, int list) pair = <obj>
# h;;
- : (int list, int list) pair -> (int list, int list) pair = <fun>
The type of the parameter of h is no longer open. The following
application cannot be typed because the argument is not of type pair.
# h (new acc_pair [] [4;5]);;
Characters 4-25:
This expression has type
('a list, int list) acc_pair =
< fst : 'a list; get1 : 'a list -> int list; get2 : int list -> 'a list;
snd : int list >
but is here used with type
(int list, int list) pair = < fst : int list; snd : int list >
Only the first object type has a method get1
Note
Parameterized classes of Objective CAML are absolutely necessary as soon as one has
methods whose type includes a type variable different from the type of
self.