Minesweeper
Let us briefly recall the object of this game: to explore a mine
field without stepping on one.
A mine field is a two dimensional array (a matrix) where some cells
contain hidden mines while others are empty. At the beginning of the
game, all the cells are closed and the player must open them one
after another. The player wins when he opens all the cells that
are empty.
Every turn, the player may open a cell or flag it as
containing a mine. If he opens a cell that contains a mine, it
blows up and the player loses. If the cell is empty, its appearance is
modified and the number of mines in the 8 neighbor cells is displayed
(thus at most 8). If the player decides to flag a cell, he cannot
open it until he removes the flag.
Figure 6.5: Screenshot.
We split the implementation of the game into three parts.
-
The abstract game, including the internal
representation of the mine field as well as the functions
manipulating this representation.
- The graphical part of the game,
including the function for displaying cells.
- The interaction between the program and the player.
The abstract mine field
This part deals with the mine field as an abstraction only, and does
not address its display.
Configuration
A mine field is defined by its dimensions
and the number of mines it contains. We group these three pieces of
data in a record and define a default configuration: 10×10
cells and 15 mines.
# type config = {
nbcols : int ;
nbrows : int ;
nbmines : int };;
# let default_config = { nbcols=10; nbrows=10; nbmines=15 } ;;
The mine field
It is natural to represent the mine field as a two dimensional array.
However, it is still necessary to specify what the cells are, and what
information their encoding should provide. The state of a cell should
answer the following questions:
-
is there a mine in this cell?
- is this cell opened (has it been seen)?
- is this cell flagged?
- how many mines are there in neighbor cells?
The last item is not mandatory, as it is possible to compute
it when it is needed. However, it is simpler to do this computation
once at the beginning of the game.
We represent a cell with a record that contains these four pieces of data.
# type cell = {
mutable mined : bool ;
mutable seen : bool ;
mutable flag : bool ;
mutable nbm : int
} ;;
The two dimensional array is an array of arrays of cells:
# type board = cell array array ;;
An iterator
In the rest of the program, we often need to iterate a function over all
the cells of the mine field. To do it generically, we define the
operator iter_cells that applies the function f,
given as an argument, to each cell of the board defined by the
configuration cf.
# let iter_cells cf f =
for i=0 to cf.nbcols-1 do for j=0 to cf.nbrows-1 do f (i,j) done done ;;
val iter_cells : config -> (int * int -> 'a) -> unit = <fun>
This is a good example of a mix between functional and imperative
programming styles, as we use a higher order function (a function
taking another function as an argument) to iterate a function that
operates through side effects (as it returns no value).
Initialization
We randomly choose which cells are mines. If c and r are
respectively the number of columns and rows of the mine field, and m
the number of mines, we need to generate m different numbers between
1 and c× r. We suppose that m £ c× r to define the
algorithm, but the program using it will need to check this condition.
The straightforward algorithm consists of starting with an empty list,
picking a random number and putting it in the list if it is not there
already, and repeating this until the list contains m numbers. We
use the following functions from the Random and
Sys modules:
-
Random.int: int -> int, picks a number
between 0 and n-1 (n is the argument) according to a random
number generator;
- Random.init: int -> unit, initializes the
random number generator;
- Sys.time: unit -> float, returns the number
of milliseconds of processor time the program used since it
started. This function will be used to initialize the random number
generator with a different seed for each game.
The modules containing these functions are described in more details
in chapter 8, pages ??
and ??.
The random mine placement function receives the number of cells
(cr) and the number of mines to place (m), and returns
a list of linear positions for the m mines.
# let random_list_mines cr m =
let cell_list = ref []
in while (List.length !cell_list) < m do
let n = Random.int cr in
if not (List.mem n !cell_list) then cell_list := n :: !cell_list
done ;
!cell_list ;;
val random_list_mines : int -> int -> int list = <fun>
With such an implementation, there is no upper bound on the number of
steps the function takes to terminate. If the random number generator
is reliable, we can only insure that the probability it does not
terminate is zero. However, all experimental uses of this function have
never failed to terminate. Thus, even though it is not guaranteed that it
will terminate, we will use it to generate the list of mined cells.
We need to initialize the random number generator so that each run of
the game does not use the same mine field. We use the processor time
since the beginning of the program execution to initialize the random
number generator.
# let generate_seed () =
let t = Sys.time () in
let n = int_of_float (t*.1000.0)
in Random.init(n mod 100000) ;;
val generate_seed : unit -> unit = <fun>
In practice, a given program very often takes the same execution time,
which results in a similar result for generate_seed for each
run. We ought to use the Unix.time function (see
chapter 18).
We very often need to know the neighbors of a given cell, during the
initialization of the mine field as well as during the game. Thus we
write a neighbors function. This function must take into
account the side and corner cells that have fewer neighbors than the
middle ones (function valid).
# let valid cf (i,j) = i>=0 && i<cf.nbcols && j>=0 && j<cf.nbrows ;;
val valid : config -> int * int -> bool = <fun>
# let neighbors cf (x,y) =
let ngb = [x-1,y-1; x-1,y; x-1,y+1; x,y-1; x,y+1; x+1,y-1; x+1,y; x+1,y+1]
in List.filter (valid cf) ngb ;;
val neighbors : config -> int * int -> (int * int) list = <fun>
The initialize_board function creates the initial mine
field. It proceeds in four steps:
-
generation of the list of mined cells;
- creation of a two dimensional array containing different cells;
- setting of mined cells in the board;
- computation of the number of mines in neighbor cells for each
cell that is not mined.
The function initialize_board uses a few local functions
that we briefly describe.
-
cell_init
- : creates an initial cell value;
- copy_cell_init
- : puts a copy of the initial cell
value in a cell of the board;
- set_mined
- : puts a mine in a cell;
- count_mined_adj
- : computes the number of mines in the
neighbors of a given cell;
- set_count
- : updates the number of mines in the neighbors
of a cell if it is not mined.
# let initialize_board cf =
let cell_init () = { mined=false; seen=false; flag=false; nbm=0 } in
let copy_cell_init b (i,j) = b.(i).(j) <- cell_init() in
let set_mined b n = b.(n / cf.nbrows).(n mod cf.nbrows).mined <- true
in
let count_mined_adj b (i,j) =
let x = ref 0 in
let inc_if_mined (i,j) = if b.(i).(j).mined then incr x
in List.iter inc_if_mined (neighbors cf (i,j)) ;
!x
in
let set_count b (i,j) =
if not b.(i).(j).mined
then b.(i).(j).nbm <- count_mined_adj b (i,j)
in
let list_mined = random_list_mines (cf.nbcols*cf.nbrows) cf.nbmines in
let board = Array.make_matrix cf.nbcols cf.nbrows (cell_init ())
in iter_cells cf (copy_cell_init board) ;
List.iter (set_mined board) list_mined ;
iter_cells cf (set_count board) ;
board ;;
val initialize_board : config -> cell array array = <fun>
Opening a cell
During a game, when the player opens a cell whose neighbors are empty
(none contains a mine), he knows that he can open the neighboring
cells without risk, and he can keep opening cells as long as he opens
cells without any mined neighbor. In order to relieve the player of
this boring process (as it is not challenging at all), our
Minesweeper opens all these cells itself. To this end, we write the
function cells_to_see that returns a list of all the
cells to open when a given cell is opened.
The algorithm needed is simple to state: if the opened cell has some
neighbors that contain a mine, then the list of cells to see consists
only of the opened cell; otherwise, the list of cells to see consists
of the neighbors of the opened cell, as well as the lists of cells to
see of these neighbors. The difficulty is in writing a program that
does not loop, as every cell is a neighbor of any of its neighbors. We
thus need to avoid processing the same cell twice.
To remember which cells were processed, we use the array of booleans
visited. Its size is the same as the mine field. The value
true for a cell of this array denotes that it was already
visited. We recurse only on cells that were not visited.
We use the auxiliary function relevant that computes two sublists
from the list of neighbors of a cell. Each one of these lists
only contains cells that do not contain a mine, that are not opened,
that are not flagged by the player, and that were not visited. The
first sublist is the list of neighboring cells who have at least one
neighbor containing a mine; the second sublist is the list of
neighboring cells whose neighbors are all empty. As these lists are
computed, all these cells are marked as visited. Notice that flagged
cells are not processed, as a flag is meant to prevent opening a
cell.
The local function cells_to_see_rec implements the
recursive search loop. It takes as an argument the list of cells to
visit, updates it, and returns the list of cells to open.
This function is called with the list consisting only of the cell
being opened, after it is marked as visited.
# let cells_to_see bd cf (i,j) =
let visited = Array.make_matrix cf.nbcols cf.nbrows false in
let rec relevant = function
[] -> ([],[])
| ((x,y) as c)::t ->
let cell=bd.(x).(y)
in if cell.mined || cell.flag || cell.seen || visited.(x).(y)
then relevant t
else let (l1,l2) = relevant t
in visited.(x).(y) <- true ;
if cell.nbm=0 then (l1,c::l2) else (c::l1,l2)
in
let rec cells_to_see_rec = function
[] -> []
| ((x,y) as c)::t ->
if bd.(x).(y).nbm<>0 then c :: (cells_to_see_rec t)
else let (l1,l2) = relevant (neighbors cf c)
in (c :: l1) @ (cells_to_see_rec (l2 @ t))
in visited.(i).(j) <- true ;
cells_to_see_rec [(i,j)] ;;
val cells_to_see :
cell array array -> config -> int * int -> (int * int) list = <fun>
At first sight, the argument of cells_to_see_rec may grow
between two consecutive calls, although the recursion is based on this
argument. It is legitimate to wonder if this function always terminates.
The way the visited array is used guarantees that a visited
cell cannot be in the result of the relevant function. Also,
all the cells to visit come from the result of the relevant
function. As the relevant function marks as visited all
the cells it returns, it returns each cell at most once, thus a cell
may be added to the list of cells to visit at most once. The number of
cells being finite, we deduce that the function terminates.
Except for graphics, we are done with our Minesweeper. Let us take a look
at the programming style we have used. Mutable structures (arrays and
mutable record fields) make us use an imperative style of loops and
assignments. However, to deal with auxiliary issues, we use lists that
are processed by functions written in a functional style. Actually,
the programming style is a consequence of the data structure that it
manipulates. The function cells_to_see is a good example:
it processes lists, and it is natural to write it in a functional
style. Nevertheless, we use an array to remember the cells that were
already processed, and we update this array imperatively. We could use
a purely functional style by using a list of visited cells instead of an
array, and check if a cell is in the list to see if it was visited.
However, the cost of such a choice is important (looking up an element
in a list is linear in the size of the list, whereas accessing an
array element takes constant time) and it does not make the program
simpler.
Displaying the Minesweeper game
This part depends on the data structures representing the state of the
game (see page ??). It consists of displaying
the different components of the Minesweeper window, as shown in
figure 6.6. To this end, we use the box drawing
functions seen on page ??.
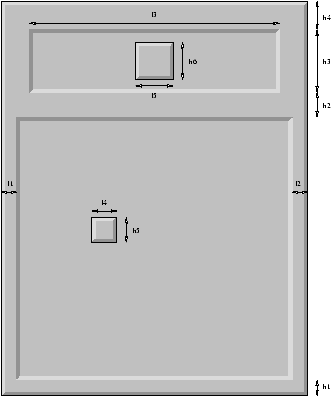
Figure 6.6:
The main window of Minesweeper.
The following parameters characterize the components of the graphical
window.
# let b0 = 3 ;;
# let w1 = 15 ;;
# let w2 = w1 ;;
# let w4 = 20 + 2*b0 ;;
# let w3 = w4*default_config.nbcols + 2*b0 ;;
# let w5 = 40 + 2*b0 ;;
|
# let h1 = w1 ;;
# let h2 = 30 ;;
# let h3 = w5+20 + 2*b0 ;;
# let h4 = h2 ;;
# let h5 = 20 + 2*b0 ;;
# let h6 = w5 + 2*b0 ;;
|
We use them to extend the basic configuration of our Minesweeper board
(value of type config). Below, we define a record type
window_config. The cf field contains the basic
configuration. We associate a box with every component of the display:
main window (field main_box), mine field (field
field_box), dialog window (field dialog_box) with two
sub-boxes (fields d1_box and d2_box), flagging
button (field flag_box) and current cell (field
current_box).
# type window_config = {
cf : config ;
main_box : box_config ;
field_box : box_config ;
dialog_box : box_config ;
d1_box : box_config ;
d2_box : box_config ;
flag_box : box_config ;
mutable current_box : box_config ;
cell : int*int -> (int*int) ;
coor : int*int -> (int*int)
} ;;
Moreover, a record of type window_config contains two functions:
-
cell: takes the coordinates of a cell and returns the
coordinates of the corresponding box;
- coor: takes the coordinates of a pixel of the window
and returns the coordinates of the corresponding cell.
Configuration
We now define a function that builds a graphical configuration (of type
window_config) according to a basic configuration (of type
config) and the parameters above. The values of the
parameters of some components depend on the value of the parameters of
other components. For instance, the global box width depends on the
mine field width, which, in turn, depends on the number of columns. To avoid
computing the same value several times, we incrementally create the
components. This initialization phase of a graphical configuration is
always a little tedious when there is no adequate primitive or
tool available.
# let make_box x y w h bw r =
{ x=x; y=y; w=w; h=h; bw=bw; r=r; b1_col=gray1; b2_col=gray3; b_col=gray2 } ;;
val make_box : int -> int -> int -> int -> int -> relief -> box_config =
<fun>
# let make_wcf cf =
let wcols = b0 + cf.nbcols*w4 + b0
and hrows = b0 + cf.nbrows*h5 + b0 in
let main_box = let gw = (b0 + w1 + wcols + w2 + b0)
and gh = (b0 + h1 + hrows + h2 + h3 + h4 + b0)
in make_box 0 0 gw gh b0 Top
and field_box = make_box w1 h1 wcols hrows b0 Bot in
let dialog_box = make_box ((main_box.w - w3) / 2)
(b0+h1+hrows+h2)
w3 h3 b0 Bot
in
let d1_box = make_box (dialog_box.x + b0) (b0 + h1 + hrows + h2)
((w3-w5)/2-(2*b0)) (h3-(2*b0)) 5 Flat in
let flag_box = make_box (d1_box.x + d1_box.w)
(d1_box.y + (h3-h6) / 2) w5 h6 b0 Top in
let d2_box = make_box (flag_box.x + flag_box.w)
d1_box.y d1_box.w d1_box.h 5 Flat in
let current_box = make_box 0 0 w4 h5 b0 Top
in { cf = cf;
main_box = main_box; field_box=field_box; dialog_box=dialog_box;
d1_box=d1_box;
flag_box=flag_box; d2_box=d2_box; current_box = current_box;
cell = (fun (i,j) -> ( w1+b0+w4*i , h1+b0+h5*j)) ;
coor = (fun (x,y) -> ( (x-w1)/w4 , (y-h1)/h5 )) } ;;
val make_wcf : config -> window_config = <fun>
Cell display
We now need to write the functions to display the cells in their
different states. A cell may be open or closed and may contain some
information. We always display (the box corresponding with) the current
cell in the game configuration (field cc_bcf).
We thus write two functions modifying the configuration of the current
cell; one closing it, the other opening it.
# let close_ccell wcf i j =
let x,y = wcf.cell (i,j)
in wcf.current_box <- {wcf.current_box with x=x; y=y; r=Top} ;;
val close_ccell : window_config -> int -> int -> unit = <fun>
# let open_ccell wcf i j =
let x,y = wcf.cell (i,j)
in wcf.current_box <- {wcf.current_box with x=x; y=y; r=Flat} ;;
val open_ccell : window_config -> int -> int -> unit = <fun>
Depending on the game phase, we may need to display some information
on the cells. We write, for each case, a specialized function.
-
Display of a closed cell:
# let draw_closed_cc wcf i j =
close_ccell wcf i j;
draw_box wcf.current_box ;;
val draw_closed_cc : window_config -> int -> int -> unit = <fun>
- Display of an opened cell with its number of neighbor mines:
# let draw_num_cc wcf i j n =
open_ccell wcf i j ;
draw_box wcf.current_box ;
if n<>0 then draw_string_in_box Center (string_of_int n)
wcf.current_box Graphics.white ;;
val draw_num_cc : window_config -> int -> int -> int -> unit = <fun>
- Display of a cell containing a mine:
# let draw_mine_cc wcf i j =
open_ccell wcf i j ;
let cc = wcf.current_box
in draw_box wcf.current_box ;
Graphics.set_color Graphics.black ;
Graphics.fill_circle (cc.x+cc.w/2) (cc.y+cc.h/2) (cc.h/3) ;;
val draw_mine_cc : window_config -> int -> int -> unit = <fun>
- Display of a flagged cell containing a mine:
# let draw_flag_cc wcf i j =
close_ccell wcf i j ;
draw_box wcf.current_box ;
draw_string_in_box Center "!" wcf.current_box Graphics.blue ;;
val draw_flag_cc : window_config -> int -> int -> unit = <fun>
- Display of a wrongly flagged cell:
# let draw_cross_cc wcf i j =
let x,y = wcf.cell (i,j)
and w,h = wcf.current_box.w, wcf.current_box.h in
let a=x+w/4 and b=x+3*w/4
and c=y+h/4 and d=y+3*h/4
in Graphics.set_color Graphics.red ;
Graphics.set_line_width 3 ;
Graphics.moveto a d ; Graphics.lineto b c ;
Graphics.moveto a c ; Graphics.lineto b d ;
Graphics.set_line_width 1 ;;
val draw_cross_cc : window_config -> int -> int -> unit = <fun>
During the game, the choice of the display function to use is done by:
# let draw_cell wcf bd i j =
let cell = bd.(i).(j)
in match (cell.flag, cell.seen , cell.mined ) with
(true,_,_) -> draw_flag_cc wcf i j
| (_,false,_) -> draw_closed_cc wcf i j
| (_,_,true) -> draw_mine_cc wcf i j
| _ -> draw_num_cc wcf i j cell.nbm ;;
val draw_cell : window_config -> cell array array -> int -> int -> unit =
<fun>
A specialized function displays all the cells at the end of the game.
It is slightly different from the previous one as all the cells are
taken as opened. Moreover, a red cross indicates the empty cells where
the player wrongly put a flag.
# let draw_cell_end wcf bd i j =
let cell = bd.(i).(j)
in match (cell.flag, cell.mined ) with
(true,true) -> draw_flag_cc wcf i j
| (true,false) -> draw_num_cc wcf i j cell.nbm; draw_cross_cc wcf i j
| (false,true) -> draw_mine_cc wcf i j
| (false,false) -> draw_num_cc wcf i j cell.nbm ;;
val draw_cell_end : window_config -> cell array array -> int -> int -> unit =
<fun>
Display of the other components
The state of the flagging mode is indicated by a box that is either at
the bottom or on top and that contain either the word ON or OFF:
# let draw_flag_switch wcf on =
if on then wcf.flag_box.r <- Bot else wcf.flag_box.r <- Top ;
draw_box wcf.flag_box ;
if on then draw_string_in_box Center "ON" wcf.flag_box Graphics.red
else draw_string_in_box Center "OFF" wcf.flag_box Graphics.blue ;;
val draw_flag_switch : window_config -> bool -> unit = <fun>
We display the purpose of the flagging button above it:
# let draw_flag_title wcf =
let m = "Flagging" in
let w,h = Graphics.text_size m in
let x = (wcf.main_box.w-w)/2
and y0 = wcf.dialog_box.y+wcf.dialog_box.h in
let y = y0+(wcf.main_box.h-(y0+h))/2
in Graphics.moveto x y ;
Graphics.draw_string m ;;
val draw_flag_title : window_config -> unit = <fun>
During the game, the number of empty cells left to be opened and the number
of cells to flag are displayed in the dialog box, to the left and
right of the flagging mode button.
# let print_score wcf nbcto nbfc =
erase_box wcf.d1_box ;
draw_string_in_box Center (string_of_int nbcto) wcf.d1_box Graphics.blue ;
erase_box wcf.d2_box ;
draw_string_in_box Center (string_of_int (wcf.cf.nbmines-nbfc)) wcf.d2_box
( if nbfc>wcf.cf.nbmines then Graphics.red else Graphics.blue ) ;;
val print_score : window_config -> int -> int -> unit = <fun>
To draw the initial mine field, we need to draw (number of rows)
× (number of columns) times the same closed cell. It is always
the same drawing, but it may take a long time, as it is necessary to
draw a rectangle as well as four trapezoids. To speed up this
initialization, we draw only one cell, take the bitmap corresponding
to this drawing, and paste this bitmap into every cell.
# let draw_field_initial wcf =
draw_closed_cc wcf 0 0 ;
let cc = wcf.current_box in
let bitmap = draw_box cc ; Graphics.get_image cc.x cc.y cc.w cc.h in
let draw_bitmap (i,j) = let x,y=wcf.cell (i,j)
in Graphics.draw_image bitmap x y
in iter_cells wcf.cf draw_bitmap ;;
val draw_field_initial : window_config -> unit = <fun>
At the end of the game, we open the whole mine field while putting
a red cross on cells wrongly flagged:
# let draw_field_end wcf bd =
iter_cells wcf.cf (fun (i,j) -> draw_cell_end wcf bd i j) ;;
val draw_field_end : window_config -> cell array array -> unit = <fun>
Finally, the main display function called at the beginning of the game
opens the graphical context and displays the initial state of all the
components.
# let open_wcf wcf =
Graphics.open_graph ( " " ^ (string_of_int wcf.main_box.w) ^ "x" ^
(string_of_int wcf.main_box.h) ) ;
draw_box wcf.main_box ;
draw_box wcf.dialog_box ;
draw_flag_switch wcf false ;
draw_box wcf.field_box ;
draw_field_initial wcf ;
draw_flag_title wcf ;
print_score wcf ((wcf.cf.nbrows*wcf.cf.nbcols)-wcf.cf.nbmines) 0 ;;
val open_wcf : window_config -> unit = <fun>
Notice that all the display primitives are parameterized by a
graphical configuration of type window_config. This makes
them independent of the layout of the components of our Minesweeper. If we
wish to modify the layout, the code still works without any
modification, only the configuration needs to be updated.
Interaction with the player
We now list what the player may do:
-
he may click on the mode box to change mode (opening or flagging),
- he may click on a cell to open it or flag it,
- he may hit the
'q' key to quit the game.
Recall that a Graphic event (Graphics.event)
must be associated with a record (Graphics.status) that
contains the current information on the mouse and keyboard when the
event occurs. An interaction with the mouse may happen on the mode
button, or on a cell of the mine field. Every other mouse event must
be ignored. In order to differentiate these mouse events, we create
the type:
# type clickon = Out | Cell of (int*int) | SelectBox ;;
Also, pressing the mouse button and releasing it are two different
events. For a click to be valid, we require that both events occur on
the same component (the flagging mode button or a cell of the mine
field).
# let locate_click wcf st1 st2 =
let clickon_of st =
let x = st.Graphics.mouse_x and y = st.Graphics.mouse_y
in if x>=wcf.flag_box.x && x<=wcf.flag_box.x+wcf.flag_box.w &&
y>=wcf.flag_box.y && y<=wcf.flag_box.y+wcf.flag_box.h
then SelectBox
else let (x2,y2) = wcf.coor (x,y)
in if x2>=0 && x2<wcf.cf.nbcols && y2>=0 && y2<wcf.cf.nbrows
then Cell (x2,y2) else Out
in
let r1=clickon_of st1 and r2=clickon_of st2
in if r1=r2 then r1 else Out ;;
val locate_click :
window_config -> Graphics.status -> Graphics.status -> clickon = <fun>
The heart of the program is the event waiting and processing loop
defined in the function loop. It is similar to the function
skel described page ??, but specifies
the mouse events more precisely. The loop ends when:
-
the player presses the q or Q key, meaning that he
wants to end the game;
- the player opens a cell containing a mine, then he loses;
- the player has opened all the cell that are empty, then he wins
the game.
We gather in a record of type minesw_cf the information
useful for the interface:
# type minesw_cf =
{ wcf : window_config; bd : cell array array;
mutable nb_flagged_cells : int;
mutable nb_hidden_cells : int;
mutable flag_switch_on : bool } ;;
The meaning of the fields is:
-
wcf: the graphical configuration;
- bd: the board;
- flag_switch_on: a boolean indicating whether flagging
mode or opening mode is on;
- nb_flagged_cells: the number of flagged cells;
- nb_hidden_cells: the number of empty cells left to open;
The main loop is implemented this way:
# let loop d f_init f_key f_mouse f_end =
f_init ();
try
while true do
let st = Graphics.wait_next_event
[Graphics.Button_down;Graphics.Key_pressed]
in if st.Graphics.keypressed then f_key st.Graphics.key
else let st2 = Graphics.wait_next_event [Graphics.Button_up]
in f_mouse (locate_click d.wcf st st2)
done
with End -> f_end ();;
val loop :
minesw_cf ->
(unit -> 'a) -> (char -> 'b) -> (clickon -> 'b) -> (unit -> unit) -> unit =
<fun>
The initialization function, cleanup function and keyboard event
processing function are very simple.
# let d_init d () = open_wcf d.wcf
let d_end () = Graphics.close_graph()
let d_key c = if c='q' || c='Q' then raise End;;
val d_init : minesw_cf -> unit -> unit = <fun>
val d_end : unit -> unit = <fun>
val d_key : char -> unit = <fun>
However, the mouse event processing function requires the use of some
auxiliary functions:
-
flag_cell: when clicking on a cell with flagging
mode on.
- ending: when ending the game. The whole mine field is
revealed, we display a message indicating whether the game was won or lost,
and we wait for a mouse or keyboard event to quit the application.
- reveal: when clicking on a cell with opening mode
on (i.e. flagging mode off).
# let flag_cell d i j =
if d.bd.(i).(j).flag
then ( d.nb_flagged_cells <- d.nb_flagged_cells -1;
d.bd.(i).(j).flag <- false )
else ( d.nb_flagged_cells <- d.nb_flagged_cells +1;
d.bd.(i).(j).flag <- true );
draw_cell d.wcf d.bd i j;
print_score d.wcf d.nb_hidden_cells d.nb_flagged_cells;;
val flag_cell : minesw_cf -> int -> int -> unit = <fun>
# let ending d str =
draw_field_end d.wcf d.bd;
erase_box d.wcf.flag_box;
draw_string_in_box Center str d.wcf.flag_box Graphics.black;
ignore(Graphics.wait_next_event
[Graphics.Button_down;Graphics.Key_pressed]);
raise End;;
val ending : minesw_cf -> string -> 'a = <fun>
# let reveal d i j =
let reveal_cell (i,j) =
d.bd.(i).(j).seen <- true;
draw_cell d.wcf d.bd i j;
d.nb_hidden_cells <- d.nb_hidden_cells -1
in
List.iter reveal_cell (cells_to_see d.bd d.wcf.cf (i,j));
print_score d.wcf d.nb_hidden_cells d.nb_flagged_cells;
if d.nb_hidden_cells = 0 then ending d "WON";;
val reveal : minesw_cf -> int -> int -> unit = <fun>
The mouse event processing function matches a value of type clickon.
# let d_mouse d click = match click with
Cell (i,j) ->
if d.bd.(i).(j).seen then ()
else if d.flag_switch_on then flag_cell d i j
else if d.bd.(i).(j).flag then ()
else if d.bd.(i).(j).mined then ending d "LOST"
else reveal d i j
| SelectBox ->
d.flag_switch_on <- not d.flag_switch_on;
draw_flag_switch d.wcf d.flag_switch_on
| Out -> () ;;
val d_mouse : minesw_cf -> clickon -> unit = <fun>
To create a game configuration, three parameters are needed: the
number of columns, the number of rows, and the number of mines.
# let create_minesw nb_c nb_r nb_m =
let nbc = max default_config.nbcols nb_c
and nbr = max default_config.nbrows nb_r in
let nbm = min (nbc*nbr) (max 1 nb_m) in
let cf = { nbcols=nbc ; nbrows=nbr ; nbmines=nbm } in
generate_seed () ;
let wcf = make_wcf cf in
{ wcf = wcf ;
bd = initialize_board wcf.cf;
nb_flagged_cells = 0;
nb_hidden_cells = cf.nbrows*cf.nbcols-cf.nbmines;
flag_switch_on = false } ;;
val create_minesw : int -> int -> int -> minesw_cf = <fun>
The launch function creates a configuration according to the numbers
of columns, rows, and mines, before calling the main event processing
loop.
# let go nbc nbr nbm =
let d = create_minesw nbc nbr nbm in
loop d (d_init d) d_key (d_mouse d) (d_end);;
val go : int -> int -> int -> unit = <fun>
The function call go 10 10 10 builds and starts a game of the
same size as the one depicted in figure 6.5.
Exercises
This program can be built as a standalone executable program.
Chapter 7 explains how to do this. Once it is
done, it is useful to be able to specify the size of the game on the
command line. Chapter 8 describes how to get
command line arguments in an Objective CAML program, and applies it to our
minesweeper (see page ??).
Another possible extension is to have the machine play to discover the
mines. To do this, one needs to be able to find the safe moves and play
them first, then compute the probabilities of presence of a mine
and open the cell with the smallest probability.