Automatic Garbage Collection
We classify automatic memory reclamation algorithms into two classes:
-
reference counters: each allocated region knows how many
references there are to it. When this number becomes zero, the region
is freed.
- sweep algorithms: starting from a set of roots,
the collection of all accessible values is traversed in a way similar
to the traversal of a directed graph.
Sweep algorithms are more commonly used in programming languages.
In effect, reference counting garbage collectors
increase the processing costs (through counter updating) even when there is no need to reclaim
anything.
Reference Counting
Each allocated region (object) is given a counter. This counter indicates the
number of pointers to the object. It is incremented each time a
reference to the object is shared. It is decremented whenever a pointer
to the object disappears. When the counter becomes zero, the object is
garbage collected.
The advantage of such a system comes from the immediate freeing of
regions that are no longer used. Aside from the systematic slowdown of
computations, reference counting garbage collectors suffer from another
disadvantage: they do not know how to process circular objects.
Suppose that Objective CAML had such a mechanism.
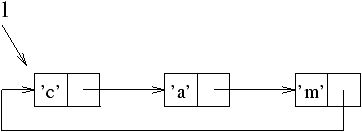
The following example constructs a temporary value l, a list of
characters of where the last element points to the cell containing
'c'. This is clearly a circular value
(figure 9.2).
# let rec l = 'c'::'a'::'m'::l in List.hd l ;;
- : char = 'c'
Figure 9.2: Memory representation of a circular list.
At the end of the calculation of this expression each element of the
list l has a counter equal to one (even the first element, for
the tail points to the head).
This value is no longer accessible and yet cannot be reclaimed because
its reference counter is not zero.
In languages equipped with memory reclamation via reference counting---such
as Python---and which allow the construction of circular
values, it is necessary to add a memory sweep algorithm.
Sweep Algorithms
Sweep algorithms allow us to explore the graph of accessible values on
the heap. This exploration uses a set of roots indicating the beginning
of the traversal. These roots are exterior to the heap, stored most
often in a stack.
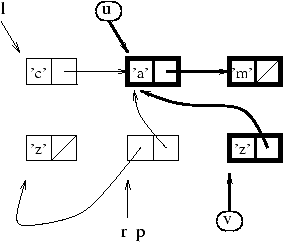
In the example in figure 9.1, we can suppose that the values
of u and v are roots. The traversal
starting from these roots constructs the graph of the values to save:
the cells and pointers marked with heavy lines
in figure 9.3.
Figure 9.3: Memory reclamation after a garbage collection.
The traversal of this graph necessitates knowing how to distinguish
immediate values from pointers in the heap. If a root points to an
integer, we must not consider this value to be the address of another
cell. In functional languages, this distinction is made by using a few
bits of each cell of the heap. We call these bits tag bits.
This is why Objective CAML integers only use 31 bits.
This option is described in Chapter 12, page ??.
We describe other solutions to the problem of distinguishing between
pointers and immediate values in this chapter,
page ??.
The two most commonly used algorithms are Mark&Sweep, which constructs the
list of the free cells in the heap, and Stop&Copy, which copies cells that
are still alive to a second memory region.
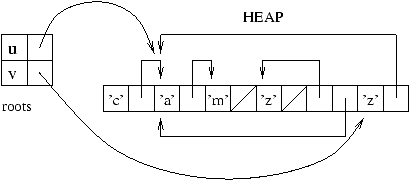
The heap should be seen as a vector of memory boxes. The representation
of the state of the heap for the example of figure 9.1
is illustrated in figure 9.4.
Figure 9.4: State of the heap.
We use the following characteristics to evaluate a sweep algorithm:
-
efficiency: does the time-complexity depend on the size of the
heap or only on the number of the living cells?
- reclamation factor: is all of the free memory usable?
- compactness: is all of the free memory usable in a single block?
- localization: are all of the different cells of a structured value
close to one another?
- memory needs: does the algorithm need to use part of the memory
when it runs?
- relocation: do values change location following a garbage collection?
Localization avoids changing memory pages when traversing a structured
value. Compactness avoids fragmentation of the heap and allows
allocations equal to the amount of available memory. The efficiency,
reclamation factor, and supplementary memory needs are intimately
linked to the time and space complexity of the algorithm.
Mark&Sweep
The idea of Mark&Sweep is to keep an up-to-date list of the free cells in the
heap called the free list. If, at the time of an allocation request,
the list is empty or no longer contains a free cell of a sufficient
size, then a Mark&Sweep occurs.
It proceeds in two stages:
-
the marking of the memory regions in use, starting from a set of
roots (called the Mark phase); then
- reclamation of the unmarked memory regions by sequentially sweeping
through the whole heap (called the Sweep phase).
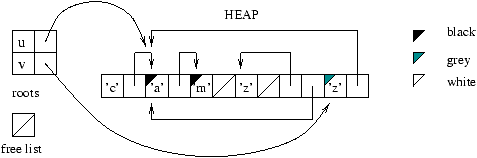
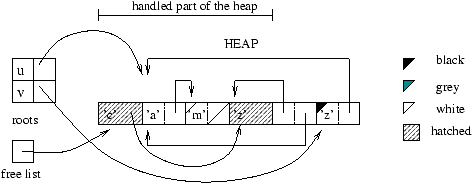
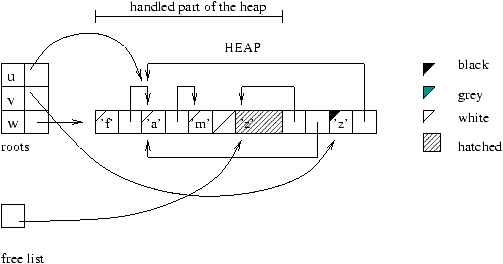
One can illustrate the memory management of Mark&Sweep by using four
``colorings'' of the heap cells: white, gray1, black, and hached.
The mark phase uses the gray; the sweep phase, the hached; and the
allocation phase, the white.
The meaning of the gray and black used by marking is as follows:
-
gray: marked cells whose descendents are not yet marked;
- black: marked cells whose descendents are also marked.
It is necessary to keep the collection of grayed cells in order to be
sure that everything has been explored. At the end of the marking each
cell is either white or black, with black cells being those that were
reached from the roots. Figure 9.5 shows an intermediate
marking stage for the example of figure 9.4: the root
u has been swept, and the sweeping of v is about to begin.
Figure 9.5: Marking phase.
It's during the sweep phase that the free list is constructed. The
sweep phase modifies the colorings as follows:
-
black becomes white, as the cell is alive;
- white becomes hached, and the cell is added to the free list.
Figure 9.6 shows the evolution of the
colors and the construction of the free list.
Figure 9.6: Sweep phase.
Characteristics of Mark&Sweep are that it:
-
depends on the size of the entire heap (Sweep phase);
- reclaims all possible memory;
- does not compact memory;
- does not guarantee localization;
- does not relocate data.
The marking phase is generally implemented by a recursive function, and
therefore uses space on the execution stack. One can give a completely
iterative version of Mark&Sweep that does not require a stack of indefinite
size, but it turns out to be less efficient than the partially recursive
version.
Finally, Mark&Sweep needs to know the size of values. The size is either
encoded in the values themselves, or deduced from the memory address by
splitting the heap into regions that allocate objects of a bounded
size. The Mark&Sweep algorithm, implemented since the very first versions of
Lisp, is still widely used. A part of the Objective CAML garbage collector
uses this algorithm.
Stop&Copy
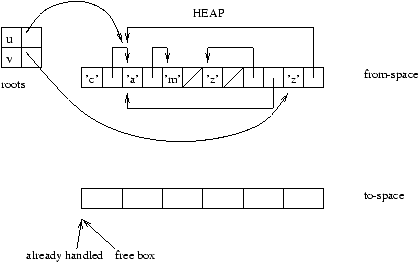
The principal idea of this garbage collector is to use a secondary
memory in order to copy and compact the memory regions to be saved. The
heap is divided into two parts: the useful part (called from-space), and the part being re-written (called to-space).
Figure 9.7: Beginning of Stop&Copy.
The algorithm is the following.
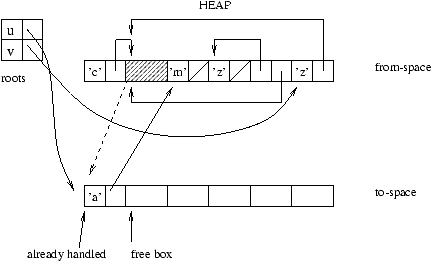
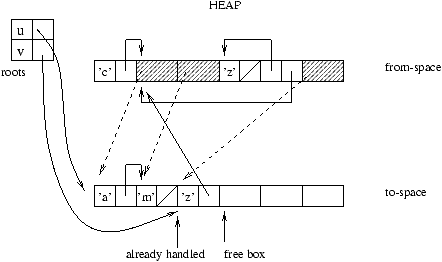
Beginning from a set of roots, each useful part of the from-space
is copied to the to-space; the new address of a relocated value
is saved (most often in its old location) in order to update all of the
other values that point to this value.
Figure 9.8: Rewriting from from-space into to-space.
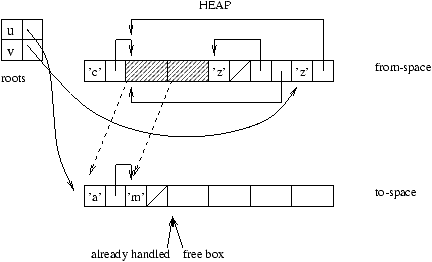
The contents of the rewritten cells gives new roots. As long as there
are unprocessed roots the algorithm continues.
Figure 9.9: New roots.
In the case of sharing, in other words, when attempting to relocate a
value that has already been relocated, it suffices to use the new
address.
Figure 9.10: Sharing.
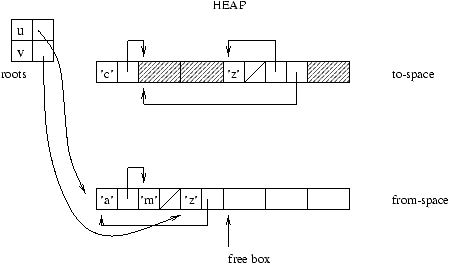
At the end of garbage collection, all of the roots are updated to point
to their new addresses. Finally, the roles of the two parts are reversed
for the next garbage collection.
Figure 9.11: Reversing the two parts.
The principal characteristics of this garbage collector are the
following:
-
it depends solely on the size of the objects to be kept;
- only half of the memory is available;
- it compacts memory;
- it may localize values (using breadth-first traversal);
- it does not use extra memory (only from-space+to-space);
- the algorithm is not recursive;
- it relocates values into the new part of memory;
Other Garbage Collectors
Many other techniques, often derived from the two preceding, have been
used: either in particular applications, e.g., the manipulation of
large matrices in symbolic calculations, or in a general way linked to
compilation techniques. Generational garbage collectors allow
optimizations based on the age of the values. Conservative garbage
collectors are used where there is not an explicit differentiation between immediate
values and pointers (for example, when one translates into C).
Finally, incremental garbage collectors allow us to avoid a noticeable
slow-down at the time of garbage collection activation.
Generational Garbage Collection
Functional programs are, in general, programs that allocate frequently.
We notice that a very large number of values have a very short
lifetime2.
On the other hand, when a value has survived several garbage
collections, it is quite likely to survive for a while longer.
In order to avoid complete traversal of the heap---as in Mark&Sweep---during
each memory reclamation, we would like to be able to traverse only
the values that have survived one or more garbage collections. Most
frequently, it is among the young values that we will recover the most
space. In order to take advantage of this property, we give objects
dates, either a time-stamp or the number of garbage collections
survived. To optimize garbage collection, we use different algorithms
according to the age of the values:
-
The garbage collections for young objects should be fast and traverse only
the younger generations.
-
The garbage collections for old objects should be rare and do well at
collecting free space from the entire memory.
As a value ages it should take part less and less in the most frequent garbage
collections. The difficulty, therefore, is taking count of only the
region of memory occupied by young objects. In a purely functional
language, that is, a language without assignment, younger objects reference older objects, and on the other hand, older
objects do not possess pointers to younger objects because they were
created before the young objects existed. Therefore, these garbage
collection techniques lend themselves well to functional languages, with
the exception of those with delayed evaluation which can in fact
evaluate the constituents of a structure after evaluating the structure
itself. On the other hand, for functional languages with assignment it
is always possible to modify part of an older object to refer to a
younger object. The problem then is to save young memory regions
referenced only by an older value. For this, it is necessary to keep an
up-to-date table of references from old objects to young objects in
order to have a correct garbage collection. We study the case of
Objective CAML in the following section.
Conservative Garbage Collectors
To this point, all of the garbage collection techniques presume knowing
how to tell a pointer from an immediate value. Note that in functional
languages with parametric polymorphism values are uniformly represented,
and in general occupy one word of memory3.
This is what allows having generic code for polymorphic functions.
However, this restriction on the range for integers may not be
acceptable. In this case, conservative garbage collectors make it
possible to avoid marking immediate values such as integers. In this
case, every value uses an entire memory word without any tag bits. In order
to avoid traversing a memory region starting from a root actually
containing an integer, we use an algorithm for discriminating between
immediate values and pointers that relies on the following observations:
-
the addresses of the beginning and end of the heap are known so
any value outside of these bounds is an immediate value;
- allocated objects are aligned on a word address. Every value that
does not correspond to such an alignment must also be an immediate value.
Thus each heap value that is valid from the point of view of being an
address into the heap is considered to be a pointer and the garbage
collector tries to keep this region, including those cases where the
value is in fact an immediate value. These cases may become very rare
by using specific memory pages according to the size of the objects.
It is not possible to guarantee that the entire unused heap is
collected. This is the principal defect of this technique. However, we
remain certain that only unused regions are reclaimed.
In general, conservative garbage collectors are conservative,
i.e., they do not relocate objects. Indeed, as the garbage
collector considers some immediate values as pointers, it would be
harmful to change their value. Nevertheless, some refinements can be
introduced for building the sets of roots, which allow to relocate
corresponding to clearly known roots.
Garbage collection techniques for ambiguous roots are often used when
compiling a functional language into C, seen here as a portable
assembler. They allow the use of immediate C values coded in a
memory word.
Incremental Garbage Collection
One of the criticisms frequently made of garbage collection is that
it stops the execution of a running program for a time that is
perceptible to the user and is unbounded.
The first is embarrassing in certain applications, for instance,
rapid-action games where the halting of the game for a few seconds is
too often prejudicial to the player, as the execution restarts without
warning. The latter is a source of loss of control for applications
which must process a certain number of events in a limited time. This
is typically the case for embedded programs which control a physical
device such as a vehicle or a machine tool. These
applications, which are real-time in the sense that they must respond in
a bounded time, most often avoid using garbage collectors.
Incremental garbage collectors must be able to be interrupted during any
one of their processing phases and be able to restart while assuring the
safety of memory reclamation. They give a sufficiently satisfactory method
for dealing with the former case, and can be used in the latter case by
enforcing a programming discipline that clearly isolates the software
components that use garbage collection from those that do not.
Let us reconsider the Mark&Sweep example and see what adaptations are
necessary in order to make it incremental. There are
essentially two:
-
how to be sure of having marked everything during the marking phase?
- how to allocate during either the marking phase or the reclamation phase?
If Mark&Sweep is interrupted in the Mark phase, it is necessary to assure
that cells allocated between the interruption of marking and its restart
are not unduly reclaimed by the Sweep that follows. For this, we
mark cells allocated during the interruption in black or gray in
anticipation.
If the Mark&Sweep is interrupted during the Sweep phase, it can continue
as usual in re-coloring the allocated cells white. Indeed, as the
Sweep phase sequentially traverses the heap, the cells allocated
during the interruption are localized before the point where the sweep
restarts, and they will not be re-examined before the next garbage
collection cycle.
Figure 9.12 shows an allocation during the reclamation phase.
The root w is created by:
# let w = 'f'::v;;
val w : char list = ['f'; 'z'; 'a'; 'm']
Figure 9.12: Allocation during reclamation.