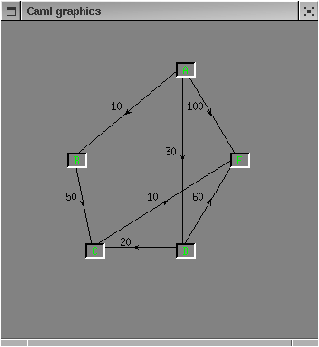
Figure 13.8: The test graph



The field size indicates the maximal number of nodes, the field ind the actual number of nodes.
# typecost=Nan|Costoffloat;;
# typeadj_mat=costarrayarray;;
# type'agraph={mutableind:int;size:int;nodes:'aarray;m:adj_mat};;
# letcreate_graphns={ind=0;size=s;nodes=Array.createsn;m=Array.create_matrixssNan};;val create_graph : 'a -> int -> 'a graph = <fun>
# letbelongs_tong=letrecauxi=(i<g.size)&((g.nodes.(i)=n)or(aux(i+1)))inaux0;;val belongs_to : 'a -> 'a graph -> bool = <fun>
# letindexng=letrecauxi=ifi>=g.sizethenraiseNot_foundelseifg.nodes.(i)=nthenielseaux(i+1)inaux0;;val index : 'a -> 'a graph -> int = <fun>
# letadd_nodeng=ifg.ind=g.sizethenfailwith"the graph is full"elseifbelongs_tongthenfailwith"the node already exists"else(g.nodes.(g.ind)<-n;g.ind<-g.ind+1);;val add_node : 'a -> 'a graph -> unit = <fun>
# letadd_edgee1e2cg=tryletx=indexe1gandy=indexe2ging.m.(x).(y)<-CostcwithNot_found->failwith"node does not exist";;val add_edge : 'a -> 'a -> float -> 'a graph -> unit = <fun>
# lettest_aho()=letg=create_graph"nothing"5inList.iter(funx->add_nodexg)["A";"B";"C";"D";"E"];List.iter(fun(a,b,c)->add_edgeabcg)["A","B",10.;"A","D",30.;"A","E",100.0;"B","C",50.;"C","E",10.;"D","C",20.;"D","E",60.];fori=0tog.ind-1dog.m.(i).(i)<-Cost0.0done;g;;val test_aho : unit -> string graph = <fun>
# leta=test_aho();;val a : string graph ={ind=5; size=5; nodes=[|"A"; "B"; "C"; "D"; "E"|];m=[|[|Cost 0; Cost 10; Nan; Cost 30; Cost ...|]; ...|]}

Figure 13.8: The test graph
SIZE 5 NODE A NODE B NODE C NODE D NODE E EDGE A B 10.0 EDGE A D 30.0 EDGE A E 100.0 EDGE B C 50. EDGE C E 10. EDGE D C 20. EDGE D E 60.To read graph files, we use the lexical analysis module Genlex. The lexical analyser is constructed from a list of keywords keywords.
# letkeywords=["SIZE";"NODE";"EDGE";"#"];;val keywords : string list = ["SIZE"; "NODE"; "EDGE"; "#"]
# letlex_linel=Genlex.make_lexerkeywords(Stream.of_stringl);;val lex_line : string -> Genlex.token Stream.t = <fun>
# letparse_linegs=matchswithparser[<'(Genlex.Kwd"SIZE");'(Genlex.Intn)>]->g:=create_graph""n|[<'(Genlex.Kwd"NODE");'(Genlex.Identname)>]->add_nodename!g|[<'(Genlex.Kwd"EDGE");'(Genlex.Idente1);'(Genlex.Idente2);'(Genlex.Floatc)>]->add_edgee1e2c!g|[<'(Genlex.Kwd"#")>]->()|[<>]->();;val parse_line : string graph ref -> Genlex.token Stream.t -> unit = <fun>
The following command constructs a graph from the file aho.dat.
# letcreate_graphname=letg=ref{ind=0;size=0;nodes=[||];m=[||]}inletic=open_innameintryprint_string("Loading "^name^": ");whiletruedoprint_string".";letl=input_lineicinparse_lineg(lex_linel)done;!gwithEnd_of_file->print_newline();close_inic;!g;;val create_graph : string -> string graph = <fun>
# letb=create_graph"PROGRAMMES/aho.dat";;Loading PROGRAMMES/aho.dat: ..............val b : string graph ={ind=5; size=5; nodes=[|"A"; "B"; "C"; "D"; "E"|];m=[|[|Nan; Cost 10; Nan; Cost 30; Cost 100|]; ...|]}
The field source contains the start node. The field already_treated indicates the nodes whose optimal path from the source is already known. The field nn indicates the total number of the graph's nodes. The vector distances holds the minimal distances between the source and the other nodes. For each node, the vector path contains the preceding node on the least cost path. The path to the source can be reconstructed from each node by using path.
# typecomp_state={paths:intarray;already_treated:boolarray;distances:costarray;source:int;nn:int};;
# letcreate_state()={paths=[||];already_treated=[||];distances=[||];nn=0;source=0};;
The value Nan plays a special role in the computations and in the comparison. We will come back to this when we have presented the main function (page ??).
# leta_costc=matchcwithNan->false|_->true;;val a_cost : cost -> bool = <fun>
# letfloat_of_costc=matchcwithNan->failwith"float_of_cost"|Costx->x;;val float_of_cost : cost -> float = <fun>
# letadd_costc1c2=match(c1,c2)withCostx,Costy->Cost(x+.y)|Nan,Costy->c2|Costx,Nan->c1|Nan,Nan->c1;;val add_cost : cost -> cost -> cost = <fun>
# letless_costc1c2=match(c1,c2)withCostx,Costy->x<y|Costx,Nan->true|_,_->false;;val less_cost : cost -> cost -> bool = <fun>
# exceptionFoundofint;;exception Found of int
# letfirst_not_treatedcs=tryfori=0tocs.nn-1doifnotcs.already_treated.(i)thenraise(Foundi)done;raiseNot_found;0withFoundi->i;;val first_not_treated : comp_state -> int = <fun>
# letleast_not_treatedpcs=letni=refpandnd=refcs.distances.(p)infori=p+1tocs.nn-1doifnotcs.already_treated.(i)thenifless_costcs.distances.(i)!ndthen(nd:=cs.distances.(i);ni:=i)done;!ni,!nd;;val least_not_treated : int -> comp_state -> int * cost = <fun>
# exceptionNo_way;;exception No_way
# letone_roundcsg=letp=first_not_treatedcsinletnp,nc=least_not_treatedpcsinifnot(a_costnc)thenraiseNo_wayelsebegincs.already_treated.(np)<-true;fori=0tocs.nn-1doifnotcs.already_treated.(i)thenifa_costg.m.(np).(i)thenletic=add_costcs.distances.(np)g.m.(np).(i)inifless_costiccs.distances.(i)then(cs.paths.(i)<-np;cs.distances.(i)<-ic)done;csend;;val one_round : comp_state -> 'a graph -> comp_state = <fun>
# letdijsg=ifbelongs_tosgthenbeginleti=indexsginletcs={paths=Array.createg.ind(-1);already_treated=Array.createg.indfalse;distances=Array.createg.indNan;nn=g.ind;source=i}incs.already_treated.(i)<-true;forj=0tog.ind-1doletc=g.m.(i).(j)incs.distances.(j)<-c;ifa_costcthencs.paths.(j)<-idone;tryfork=0tocs.nn-2doignore(one_roundcsg)done;cswithNo_way->csendelsefailwith"dij: node unknown";;val dij : 'a -> 'a graph -> comp_state = <fun>
# letg=test_aho();;
# letr=dij"A"g;;
# r.paths;;- : int array = [|0; 0; 3; 0; 2|]
# r.distances;;- : cost array = [|Cost 0; Cost 10; Cost 50; Cost 30; Cost 60|]
This recursive function uses the command stack to display the nodes in the right order. Note that the use of the format "a" requires the function parameter f to preserve the polymorphism of the graphs for the display.
# letdisplay_statef(g,st)dest=ifbelongs_todestgthenletd=indexdestginletrecauxis=ifis=st.sourcethenPrintf.printf"%a"fg.nodes.(is)else(letold=st.paths.(is)inauxold;Printf.printf" -> (%4.1f) %a"(float_of_costg.m.(old).(is))fg.nodes.(is))inifnot(a_costst.distances.(d))thenPrintf.printf"no way\n"else(auxd;Printf.printf" = %4.1f\n"(float_of_costst.distances.(d)));;val display_state :(out_channel -> 'a -> unit) -> 'a graph * comp_state -> 'a -> unit = <fun>
# display_state(funxy->Printf.printf"%s!"y)(a,r)"E";;A! -> (30.0) D! -> (20.0) C! -> (10.0) E! = 60.0- : unit = ()
The fields g and w correspond to the graph and to the table of weak pointers, pointing to the computation states for each possible source.
# type'acomp_graph={g:'agraph;w:comp_stateWeak.t};;
# letcreate_comp_graphg={g=g;w=Weak.createg.ind};;val create_comp_graph : 'a graph -> 'a comp_graph = <fun>
# letdij_quickscg=leti=indexscg.ginmatchWeak.getcg.wiwithNone->letcs=dijscg.ginWeak.setcg.wi(Somecs);cs|Somecs->cs;;val dij_quick : 'a -> 'a comp_graph -> comp_state = <fun>
# letcg_a=create_comp_graphainletr=dij_quick"A"cg_aindisplay_state(funxy->Printf.printf"%s!"y)(a,r)"E";;A! -> (30.0) D! -> (20.0) C! -> (10.0) E! = 60.0- : unit = ()
# letexe_timefgss=lett0=Sys.time()inPrintf.printf"Start (%5.2f)\n"t0;List.iter(funs->ignore(fsg))ss;lett1=Sys.time()inPrintf.printf"End (%5.2f)\n"t1;Printf.printf"Duration = (%5.2f)\n"(t1-.t0);;val exe_time : ('a -> 'b -> 'c) -> 'b -> 'a list -> unit = <fun>
# letss=letss0=ref[]inleti0=int_of_char'A'inletnew_si=Char.escaped(char_of_int(i0+i))infori=0to20000doss0:=(new_s(Random.inta.size))::!ss0done;!ss0;;val ss : string list =["A"; "B"; "D"; "A"; "E"; "C"; "B"; "B"; "D"; "E"; "B"; "E"; "C"; "E"; "E";"D"; "D"; "A"; "E"; ...]
# Printf.printf"Function dij :\n";exe_timedijass;;Function dij :Start ( 1.14)End ( 1.46)Duration = ( 0.32)- : unit = ()
# Printf.printf"Function dij_quick :\n";exe_timedij_quick(create_comp_grapha)ss;;Function dij_quick :Start ( 1.46)End ( 1.50)Duration = ( 0.04)- : unit = ()
##load"PROGRAMMES/awi.cmo";;
# type'agg={mutablesrc:'a*Awi.component;mutabledest:'a*Awi.component;pos:(int*int)array;cg:'acomp_graph;mutablestate:comp_state;mutablemain:Awi.component;to_string:'a->string;from_string:string->'a};;
# letcreate_ggcgvpostsfs={src=cg.g.nodes.(0),Awi.empty_component;dest=cg.g.nodes.(0),Awi.empty_component;pos=vpos;cg=cg;state=create_state();main=Awi.empty_component;to_string=ts;from_string=fs};;val create_gg :'a comp_graph ->(int * int) array -> ('a -> string) -> (string -> 'a) -> 'a gg = <fun>
# letrotatela=letca=cosaandsa=sinainList.map(function(x,y)->(x*.ca+.-.y*.sa,x*.sa+.y*.ca))l;;val rotate : (float * float) list -> float -> (float * float) list = <fun>
# lettranslatel(tx,ty)=List.map(function(x,y)->(x+.tx,y+.ty))l;;val translate :(float * float) list -> float * float -> (float * float) list = <fun>
# letdisplay_arrow(mx,my)a=lettriangle=[(5.,0.);(-3.,3.);(1.,0.);(-3.,-3.);(5.,0.)]inlettr=rotatetriangleainletttr=translatetr(mx,my)inlettt=List.map(function(x,y)->(int_of_floatx,int_of_floaty))ttrinGraphics.fill_poly(Array.of_listtt);;val display_arrow : float * float -> float -> unit = <fun>
# letdisplay_label(mx,my)alab=let(sx,sy)=Graphics.text_sizelabinletpos=[float(-sx/2),float(-sy)]inletpr=rotateposainletpt=translatepr(mx,my)inletpx,py=List.hdptinletox,oy=Graphics.current_point()inGraphics.moveto((int_of_floatmx)-sx-6)((int_of_floatmy));Graphics.draw_stringlab;Graphics.movetooxoy;;val display_label : float * float -> float -> string -> unit = <fun>
# letdisplay_edgeggcolij=letg=gg.cg.ginletx,y=gg.main.Awi.x,gg.main.Awi.yinifa_costg.m.(i).(j)then(let(a1,b1)=gg.pos.(i)and(a2,b2)=gg.pos.(j)inletx0,y0=x+a1,y+b1andx1,y1=x+a2,y+b2inletrxm=(float(x1-x0))/.2.andrym=(float(y1-y0))/.2.inletxm=(floatx0)+.rxmandym=(floaty0)+.ryminGraphics.set_colorcol;Graphics.movetox0y0;Graphics.linetox1y1;leta=atan2rymrxmindisplay_arrow(xm,ym)a;display_label(xm,ym)a(string_of_float(float_of_costg.m.(i).(j))));;val display_edge : 'a gg -> Graphics.color -> int -> int -> unit = <fun>
# letrecdisplay_shortest_pathggcoldest=letg=gg.cg.ginifbelongs_todestgthenletd=indexdestginletrecauxis=ifis=gg.state.sourcethen()else(letold=gg.state.paths.(is)indisplay_edgeggcololdis;auxold)inifnot(a_costgg.state.distances.(d))thenPrintf.printf"no way\n"elseauxd;;val display_shortest_path : 'a gg -> Graphics.color -> 'a -> unit = <fun>
#letdisplay_gggg()=Awi.display_rectgg.main();fori=0togg.cg.g.ind-1doforj=0togg.cg.g.ind-1doifi<>jthendisplay_edgegg(Graphics.black)ijdonedone;ifsndgg.dest!=Awi.empty_componentthendisplay_shortest_pathggGraphics.red(fstgg.dest);;val display_gg : 'a gg -> unit -> unit = <fun>
# letinverseb=letgc=Awi.get_gcbinletfcol=Awi.get_gc_fcolgcandbcol=Awi.get_gc_bcolgcinAwi.set_gc_bcolgcfcol;Awi.set_gc_fcolgcbcol;;val inverse : Awi.component -> unit = <fun>
# letaction_clicknodeggbbs=let(s1,s)=gg.srcand(s2,d)=gg.destinifs==Awi.empty_componentthen(gg.src<-(node,b);inverseb)elseifd==Awi.empty_componentthen(inverseb;gg.dest<-(node,b);gg.state<-dij_quicks1gg.cg;display_shortest_pathgg(Graphics.red)node)else(inverses;inversed;gg.dest<-(s2,Awi.empty_component);gg.src<-node,b;inverseb);;val action_click : 'a -> 'a gg -> Awi.component -> 'b -> unit = <fun>
The buttons are created automatically. They are positioned on the main window.
# letmain_gggggwghloptlopt2=letgc=Awi.make_default_context()inAwi.set_gcgclopt;(* compute the maximal button size *)letvs=Array.mapgg.to_stringgg.cg.g.nodesinletvsize=Array.mapGraphics.text_sizevsinletw=Array.fold_right(fun(x,y)->maxx)vsize0andh=Array.fold_right(fun(x,y)->maxy)vsize0in(* create the main panel *)gg.main<-Awi.create_paneltruegwghlopt;gg.main.Awi.display<-display_gggg;(* create the buttons *)letvb_bs=Array.map(funx->x,Awi.create_button(" "^(gg.to_stringx)^" ")lopt)gg.cg.g.nodesinletf_act_b=Array.map(fun(x,(b,bs))->letac=action_clickxggbinAwi.set_bs_actionbsac)vb_bsinletbb=Array.map(function(_,(b,_))->Awi.create_borderblopt2)vb_bsinArray.iteri(funi(b)->letx,y=gg.pos.(i)inAwi.add_componentgg.mainb["PosX",Awi.Iopt(x-w/2);"PosY",Awi.Iopt(y-h/2)])bb;();;val main_gg :'a gg ->int ->int -> (string * Awi.opt_val) list -> (string * Awi.opt_val) list -> unit =<fun>
# letidx=x;;
# letpos=[|200,300;80,200;100,100;200,100;260,200|];;
# letgg=create_gg(create_comp_graph(test_aho()))posidid;;
# main_gggg400400["Background",Awi.Copt(Graphics.rgb130130130);"Foreground",Awi.CoptGraphics.green]["Relief",Awi.Sopt"Top";"Border_size",Awi.Iopt2];;
Figure 13.9 shows the computed path between the nodes "A" and "E". The edges on the path have changed their color.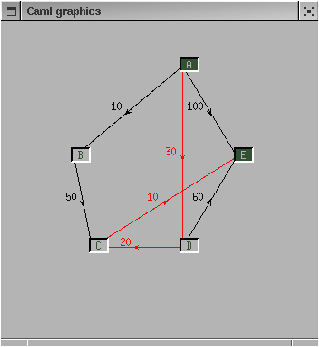
Figure 13.9: Selecting the nodes for a search
# typeg_info={npos:(int*int)array;mutableopt:Awi.lopt;mutableg_w:int;mutableg_h:int};;
# letkey2=["HEIGHT";"LENGTH";"POSITION";"COLOR"];;val key2 : string list = ["HEIGHT"; "LENGTH"; "POSITION"; "COLOR"]
# letlex2l=Genlex.make_lexerkey2(Stream.of_stringl);;val lex2 : string -> Genlex.token Stream.t = <fun>
# letpars2ggis=matchswithparser[<'(Genlex.Kwd"HEIGHT");'(Genlex.Inti)>]->gi.g_h<-i|[<'(Genlex.Kwd"LENGTH");'(Genlex.Inti)>]->gi.g_w<-i|[<'(Genlex.Kwd"POSITION");'(Genlex.Idents);'(Genlex.Inti);'(Genlex.Intj)>]->gi.npos.(indexsg)<-(i,j)|[<'(Genlex.Kwd"COLOR");'(Genlex.Idents);'(Genlex.Intr);'(Genlex.Intg);'(Genlex.Intb)>]->gi.opt<-(s,Awi.Copt(Graphics.rgbrgb))::gi.opt|[<>]->();;val pars2 : string graph -> g_info -> Genlex.token Stream.t -> unit = <fun>
# letcreate_gg_graphname=letg=create_graphnameinletgi={npos=Array.createg.size(0,0);opt=[];g_w=0;g_h=0;}inletic=open_innameintryprint_string("Loading (pass 2) "^name^" : ");whiletruedoprint_string".";letl=input_lineicinpars2ggi(lex2l)done;g,giwithEnd_of_file->print_newline();close_inic;g,gi;;val create_gg_graph : string -> string graph * g_info = <fun>
# letcreate_appname=letg,gi=create_gg_graphnameinletsize=(string_of_intgi.g_w)^"x"^(string_of_intgi.g_h)inGraphics.open_graph(" "^size);letgg=create_gg(create_comp_graphg)gi.nposididinmain_gggggi.g_wgi.g_h["Background",Awi.Copt(Graphics.rgb130130130);"Foreground",Awi.CoptGraphics.green]["Relief",Awi.Sopt"Top";"Border_size",Awi.Iopt2];gg;;val create_app : string -> string gg = <fun>
# letmain()=if(Array.lengthSys.argv)<>2thenPrintf.printf"Usage: dij.exe filename\n"elseletgg=create_appSys.argv.(1)inAwi.looptruefalsegg.main;;val main : unit -> unit = <fun>
ocamlc -custom -o dij.exe graphics.cma awi.cmo graphs.ml \
-cclib -lgraphics -cclib -L/usr/X11/lib -cclib -lX11
Compiling standalone applications using the Graphics library
is described in chapters 5 and 7. 

